图
{Back to Index}

Table of Contents

1 基本概念

图由 顶点 (vertex) 和 边 (edge) 组成，通常表示为 G=(V,E) 。

1.1 有向图

1.1.1 出度/入度

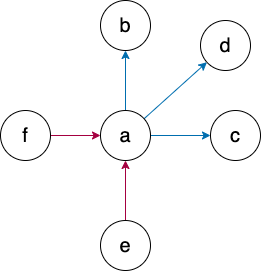
graph_degree.png

Figure 1: a 的出度为 3 ，入度为 2

1.2 无向图

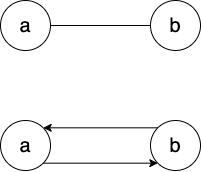
graph_undirect.png

Figure 2: 无向图与有向图的转换

1.3 有权图

2 常见实现方式

2.1 邻接矩阵

使用一维数组存放顶点信息，二维数组存放边信息。

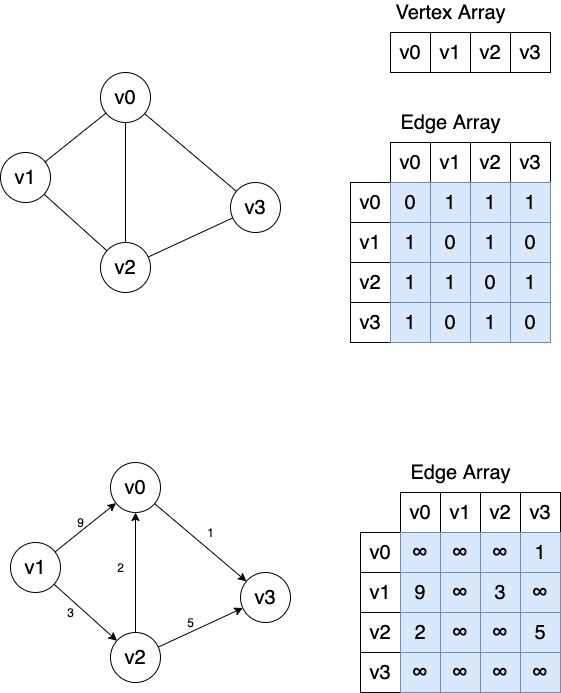
adjacent_matrix.png

Figure 3: 使用邻接矩阵实现图

2.2 邻接表

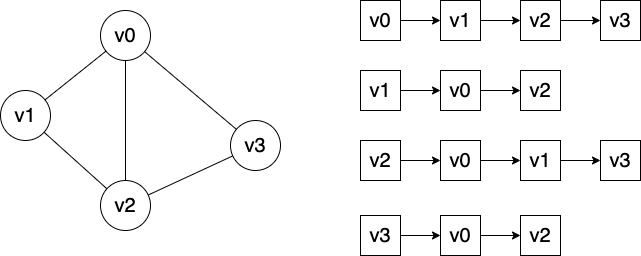
adjacent_list.png

Figure 4: 使用链表来表达图的结构

2.3 邻接表改进 ✓

2.3.1 接口

public interface Graph<V> {

    void addVertex(V v);
    void addEdge(V from, V to);
    void addEdge(V from, V to, int weight);

    void removeVertex(V v);
    void removeEdge(V from, V to);

    int edgeSize();
    int verticesSize();


    public static class Vertex<V> {
        V value;
        Set<Edge<V>> inEdges = new HashSet<>();
        Set<Edge<V>> outEdges = new HashSet<>();
    }

    public static class Edge<V> {
        Vertex<V> from;
        Vertex<V> to;
        int weight = 0;
    }
}

2.3.2 实现

public class GraphImpl<V> implements Graph<V> {

    Map<V, Vertex<V>> vertices = new HashMap<>();
    Set<Edge<V>> edges = new HashSet<>();

    @Override
    public void addVertex(V v) {
        if (vertices.containsKey(v)) return;
        vertices.put(v, Vertex.of(v));
    }

    @Override
    public void addEdge(V from, V to) {
        addEdge(from, to, 0);
    }

    @Override
    public void addEdge(V from, V to, int weight) {
        Vertex<V> fromVertex = vertices.get(from);
        if (fromVertex == null) {
            fromVertex = Vertex.of(from);
            vertices.put(from, fromVertex);
        }
        Vertex<V> toVertex = vertices.get(to);
        if (toVertex == null) {
            toVertex = Vertex.of(to);
            vertices.put(to, toVertex);
        }

        Edge<V> edge = Edge.of(fromVertex, toVertex, weight);
        edges.remove(edge);
        edges.add(edge);

        fromVertex.outEdges.remove(edge);
        fromVertex.outEdges.add(edge);

        toVertex.inEdges.remove(edge);
        toVertex.inEdges.add(edge);
    }

    @Override
    public void removeVertex(V v) {
        Vertex<V> vertex = vertices.get(v);
        if (vertex == null) return;
        vertex.outEdges.stream()
            .map(e -> e.to)
            .collect(Collectors.toList())
            .forEach(to -> removeEdge(vertex.value, to.value));

        vertex.inEdges.stream()
            .map(e -> e.from)
            .collect(Collectors.toList())
            .forEach(from -> removeEdge(from.value, vertex.value));
        vertices.remove(v);
    }

    @Override
    public void removeEdge(@NonNull V from, @NonNull V to) {
        Vertex<V> fromVertex = vertices.get(from);
        if (fromVertex == null) return;
        Vertex<V> toVertex = vertices.get(to);
        if (toVertex == null) return;
        Edge<V> edge = Edge.of(fromVertex, toVertex);
        fromVertex.outEdges.remove(edge);
        toVertex.inEdges.remove(edge);
        edges.remove(edge);
    }

    @Override
    public int edgeSize() {
        return edges.size();
    }

    @Override
    public int verticesSize() {
        return vertices.size();
    }
}

3 遍历

3.1 广度优先 (BFS)

public void bfs(V v, Consumer<V> visitor) {
    Set<Vertex<V>> visited = new HashSet<>();
    Queue<Vertex<V>> queue = new LinkedList<>();
    Vertex<V> startNode = vertices.get(v);
    if (startNode == null) return;
    queue.offer(startNode);
    visited.add(startNode);
    while (!queue.isEmpty()) {
        Vertex<V> node = queue.poll();
        visitor.accept(node.value);
        node.outEdges.stream()
            .map(e -> e.to)
            .filter(to -> !visited.contains(to))
            .collect(Collectors.toList())
            .forEach(n -> {
                    queue.offer(n);
                    visited.add(n);
                });
    }
}

3.2 深度优先 (DFS)

类似于二叉树的前序遍历。 

public void dfs(V v, Consumer<V> visitor) {
    Set<Vertex<V>> visited = new HashSet<>();
    Stack<Vertex<V>> stack = new Stack<>();
    Vertex<V> startNode = vertices.get(v);
    if (startNode == null) return;
    stack.push(startNode);
    visitor.accept(startNode.value);
    visited.add(startNode);
    while (!stack.isEmpty()) {
        Vertex<V> node = stack.pop();
        for (Edge<V> edge : node.outEdges) {
            Vertex<V> to = edge.to;
            if (visited.contains(to)) continue;
            stack.push(node);
            stack.push(to);
            visited.add(to);
            visitor.accept(to.value);
            break;
        }
    }
}

4 AOV (Activity On Vertex Network)

以顶点表示活动，以有向边表示活动之间的先后关系，这样的图称为 AOV ，AOV 必须是 有向无环图 。

4.1 拓扑排序

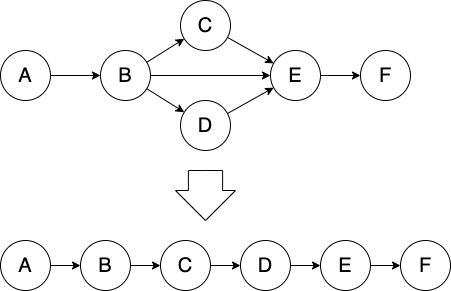
aov_topo.png

Figure 5: 拓扑排序

4.1.1 卡恩算法(可判断是否存在环路)

  1. 收集所有入度为零的顶点，然后把这些顶点从图中删除
  2. 重复上述操作，直至找不到入度为零的顶点
  3. 如果找不到入度为零的顶点，而收集到的顶点数量又小于顶点总数，则说明 图中存在环 ，无法完成拓扑排序
public List<V> aov() {
    Map<Vertex<V>, Integer> inDegreeMap = new HashMap<>();
    vertices.values().forEach(v -> inDegreeMap.put(v, v.inEdges.size()));
    List<V> result = new ArrayList<>();
    Queue<Vertex<V>> queue = new LinkedList<>();
    while (result.size() != verticesSize()) {
        for (Vertex<V> v : inDegreeMap.keySet()) {
            if (inDegreeMap.get(v) == 0) {
                queue.offer(v);
            }
        }
        if (queue.isEmpty()) throw new RuntimeException("There is a LOOP in graph");
        while (!queue.isEmpty()) {
            Vertex<V> vertex = queue.poll();
            inDegreeMap.remove(vertex);
            result.add(vertex.value);
            for (Edge<V> outEdge : vertex.outEdges) {
                inDegreeMap.put(outEdge.to, inDegreeMap.get(outEdge.to) - 1);
            }
        }
    }
    return result;
}

5 生成树(Spanning Tree)

生成树是一个连通图， 含有图中全部 n 个顶点，而只有 n - 1 条边。

5.1 最小生成树

所有生成树中， 总权值最小 的那棵树。

最小生成树适用于 有权 的 无向 连通 图。
(如果图中每条边的权值互不相同，则最小生成树唯一，否则不唯一)

5.1.1 Prim 算法

5.1.1.1 切分定理

对于 任意切分 ，横切边中权值最小的边必然属于最小生成树。

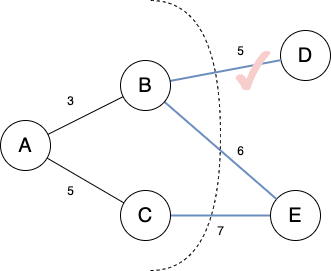
prim_cutting.png

Figure 6: 切分定理

5.1.1.2 执行流程

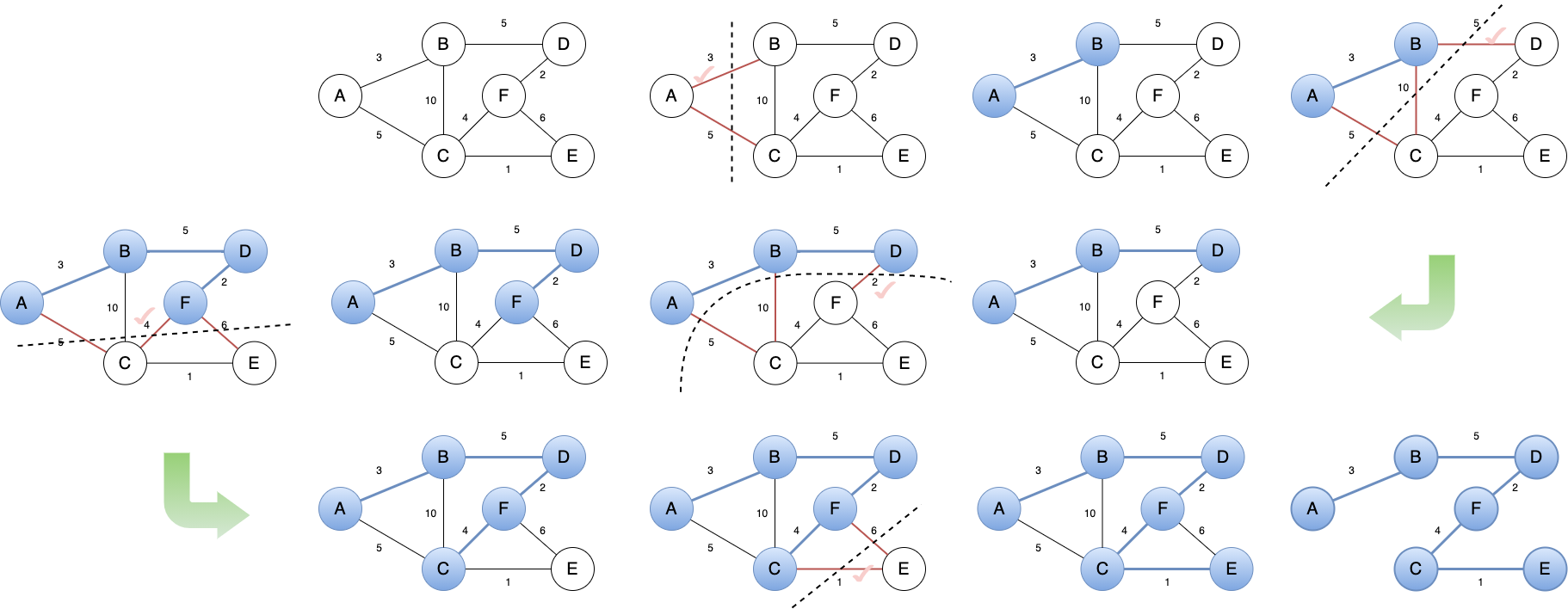
prim_cutting_exec.png

Figure 7: Prim 算法执行步骤

横切边都是 选中路径上的顶点 与 待选路径上的顶点 之间的边。 

public List<EdgeInfo<V>> mst() {
    if (verticesSize() == 0) return null;

    Vertex<V> vertex = vertices.values().iterator().next();
    PriorityQueue<Edge<V>> heap = new PriorityQueue<>(Comparator.comparingInt(Edge::getWeight));
    Set<Vertex<V>> verticesAlongThePath = new HashSet<>();

    vertex.outEdges.forEach(heap::offer);
    verticesAlongThePath.add(vertex);
    List<EdgeInfo<V>> result = new ArrayList<>();

    while (result.size() != verticesSize() - 1) {
        Edge<V> minEdge = heap.poll();
        if (verticesAlongThePath.contains(minEdge.to)) continue;
        result.add(minEdge.toEdgeInfo());
        verticesAlongThePath.add(minEdge.to);
        minEdge.to.outEdges.stream()
            .filter(e -> !verticesAlongThePath.contains(e.to))
            .forEach(heap::offer);
    }

    return result;
}

5.1.2 Kruskal 算法

从切分定理可以推得： 权重最小的两条边必定会出现在最终的生成树中，而第三小的边不一定，因为可能导致环路。
因此 Kruskal 算法的思想是按照边的权重顺序从小到大加入生成树中，如果加入的边会导致环路，则不加入该边， 直至树中含有 n - 1 条边为止(n 是顶点数量)。

这里可以使用 并查集 1 数据结构来判断是否构成环路。

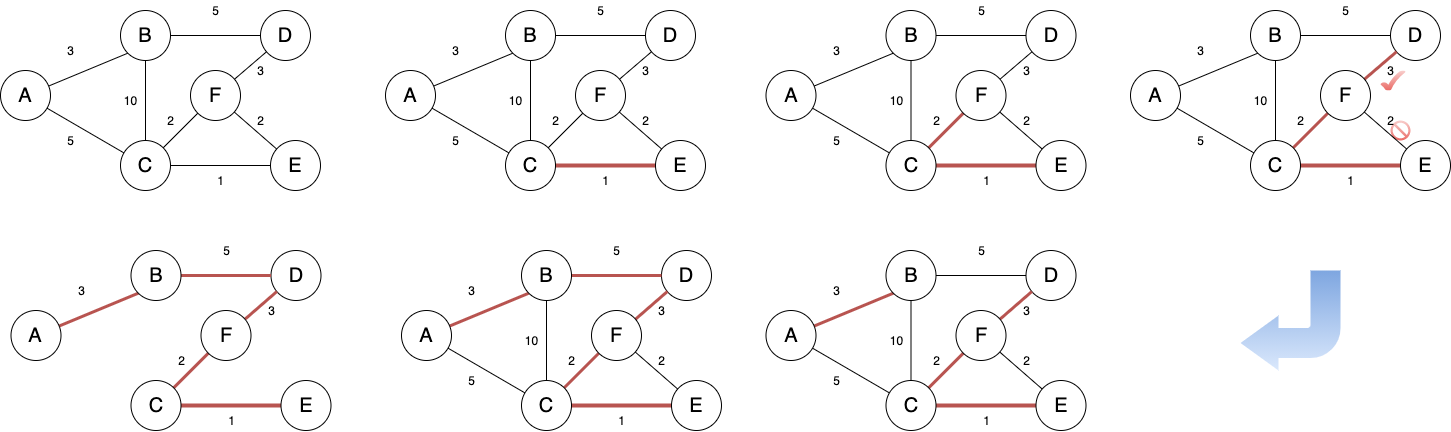
mst_kruskal.png

Figure 8: Kruskal 执行过程

public Set<EdgeInfo<V>> mst() {
    if (verticesSize() == 0) return null;
    HashSet<Vertex<V>> verticesSet = new HashSet<>(this.vertices.values());
    UnionFind<Vertex<V>> uf = new UnionFind<>(verticesSet);
    PriorityQueue<Edge<V>> heap = new PriorityQueue<>(Comparator.comparingInt(Edge::getWeight));
    edges.forEach(heap::offer);
    Set<EdgeInfo<V>> result = new HashSet<>();
    while (result.size() < verticesSize()) {
        Edge<V> edge = heap.poll();
        if (uf.inSameSet(edge.from, edge.to)) continue;
        result.add(edge.info());
        uf.union(edge.from, edge.to);
    }
    return result;
}

6 最短路径算法

最短路径指的是两个顶点之间权值之和最小的路径，适用于有向图和无向图，但 不能有负权环 。

最短路径算法可分为 单源 和 多源 两种类型。

单源最短路径算法，其输出结果为一个源顶点到其他顶点的最短路径集合，且并不是所有单源算法都支持负权边。 单源类算法包括 Dijkstra (不支持负权边) 和 Bellman Ford (支持负权边) 等算法。

多源最短路径算法(Floyd)，能够求出任意两个顶点间的最短路径，且支持负权边。

6.1 Dijkstra [O(ElogV)]

Dijkstra 算法的思想是将节点想象成放在桌面的石头，边的权值想象成连接石头的绳子长度，将源头向上提起，直至全部石头都被提起：

  • 绷直的绳子的长度代表了源头到其他石头（节点）的最短路径
  • 一旦你石头离开了桌面就代表确定了最短路径
  • 后离开桌面的石头都是被先离开桌面的石头拉起的

该算法的执行过程为：

  • 从路径权值表中选出路径权值最小的记录，目标节点即为选中节点，该条记录即为源到该目标节点的最短路径
  • 对选中节点的出度进行松弛操作
  • 重复上述两个步骤，直至得到所有最短路径
以下图为例，假设 A 为源节点，当确定了 A 到 D 的最短路径后，所谓的松弛操作指的是用 DC ，DE 边的权值来更新 A 到 C ，A 到 E 的最短路径。
因此松弛操作的意义是更新源节点到其他节点间的路径，尝试找出更短的路径。

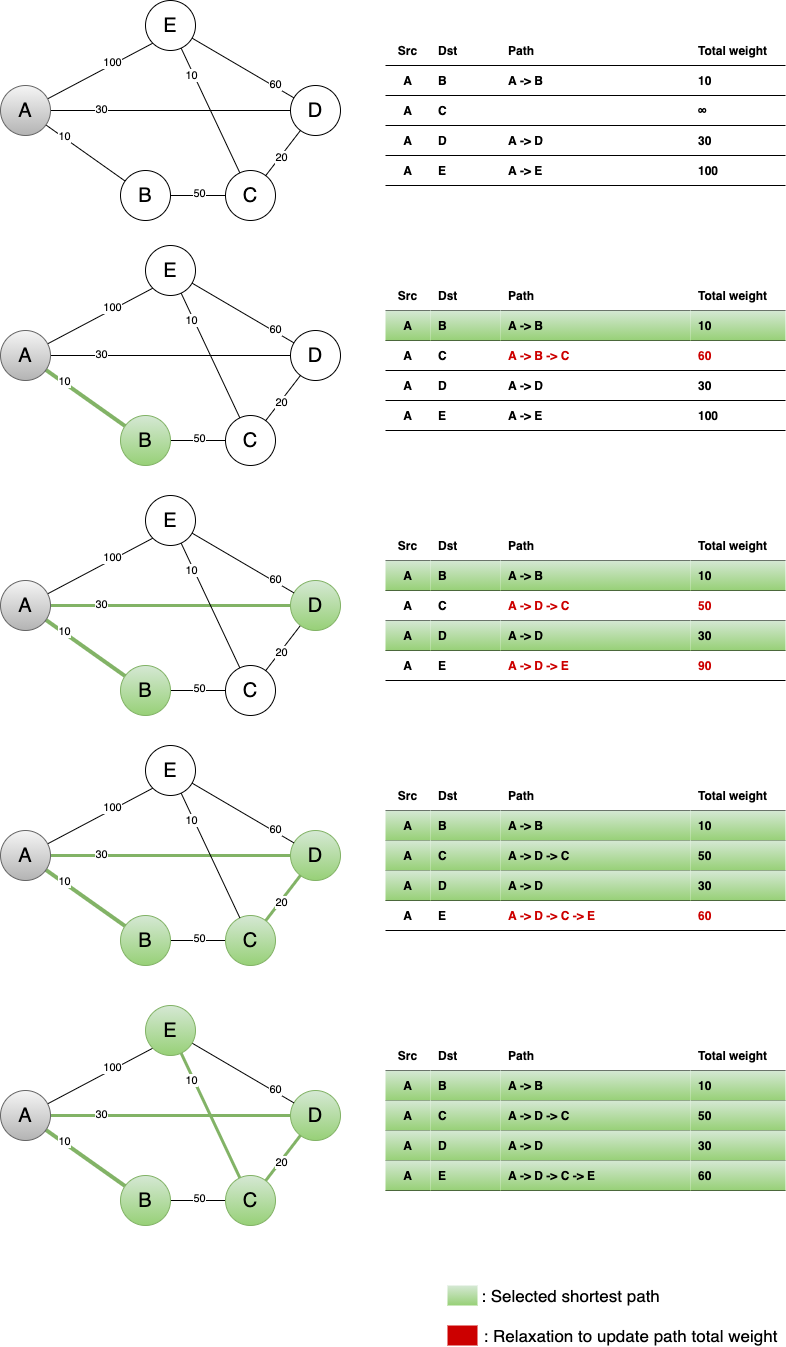
dijkstra.png

Figure 9: 执行过程

public Map<V, PathInfo<V>> shortestPathDijkstra(V source) {
    Vertex<V> sourceVertex = vertices.get(source);
    if (sourceVertex == null) return null;
    Map<Vertex<V>, PathInfo<V>> pathMap = new HashMap<>();
    if (sourceVertex.outEdges.isEmpty()) return null;
    sourceVertex.outEdges.forEach(e -> pathMap.put(e.to, new PathInfo<>(Lists.newArrayList(e.info()), e.weight)));
    Map<V, PathInfo<V>> selectedPath = new HashMap<>();

    while (!pathMap.isEmpty()) {
        Map.Entry<Vertex<V>, PathInfo<V>> entry = selectShortestPath(pathMap);
        Vertex<V> selectedVertex = entry.getKey();
        selectedPath.put(selectedVertex.value, entry.getValue());
        for (Edge<V> outEdge : selectedVertex.outEdges) {
            if (outEdge.to == sourceVertex) continue;
            if (selectedPath.containsKey(outEdge.to.value)) continue;
            doRelaxation(outEdge, pathMap, selectedPath.get(selectedVertex.value));
        }
    }

    return selectedPath;
}

private void doRelaxation(Edge<V> outEdge, Map<Vertex<V>, PathInfo<V>> pathMap, PathInfo<V> selectedPath) {
    Vertex<V> to = outEdge.to;
    if (!pathMap.containsKey(to)) {
        pathMap.put(to, new PathInfo<>(Lists.newArrayList(selectedPath.getEdges()), outEdge.weight + selectedPath.weight));
        return;
    }
    PathInfo<V> oldPath = pathMap.get(to);
    if (selectedPath.weight + outEdge.weight < oldPath.weight) {
        ArrayList<EdgeInfo<V>> newEdges = Lists.newArrayList(selectedPath.getEdges());
        newEdges.add(outEdge.info());
        oldPath.setEdges(newEdges);
        oldPath.weight = selectedPath.weight + outEdge.weight;
    }
}

private Map.Entry<Vertex<V>, PathInfo<V>> selectShortestPath(Map<Vertex<V>, PathInfo<V>> pathMap) {
    Map.Entry<Vertex<V>, PathInfo<V>> entry = pathMap.entrySet().stream()
        .min(Comparator.comparingInt(e-> e.getValue().getWeight())).get();
    pathMap.remove(entry.getKey());
    return entry;
}

6.1.1 算法局限性

使用该算法的前提是 不能有负权边 。

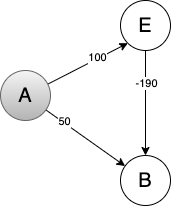
dijkstra_non_negative.png

Figure 10: Dijkstra 算法不适用有负权边的情况

以上图为例，源到节点 B 的最短路径在一开始就确定了(A->B)。 但是当拉起节点 E 后发现 A->E->B 的路径更短，按照 Dijkstra 的算法思想和执行流程，最短路径一旦确定就不能再更新了。 因此在有负权边的情况下，Dijkstra 算法并不准确。

6.2 Bellman Ford [O(EV)]

该算法不仅 支持负权边 的情况，还能用来 检测是否有负权环

算法的理论是：只要对所有的边进行 V - 1 轮 松弛操作 (V是节点数量)，就可以得到源节点到所有其他节点的最短路径。

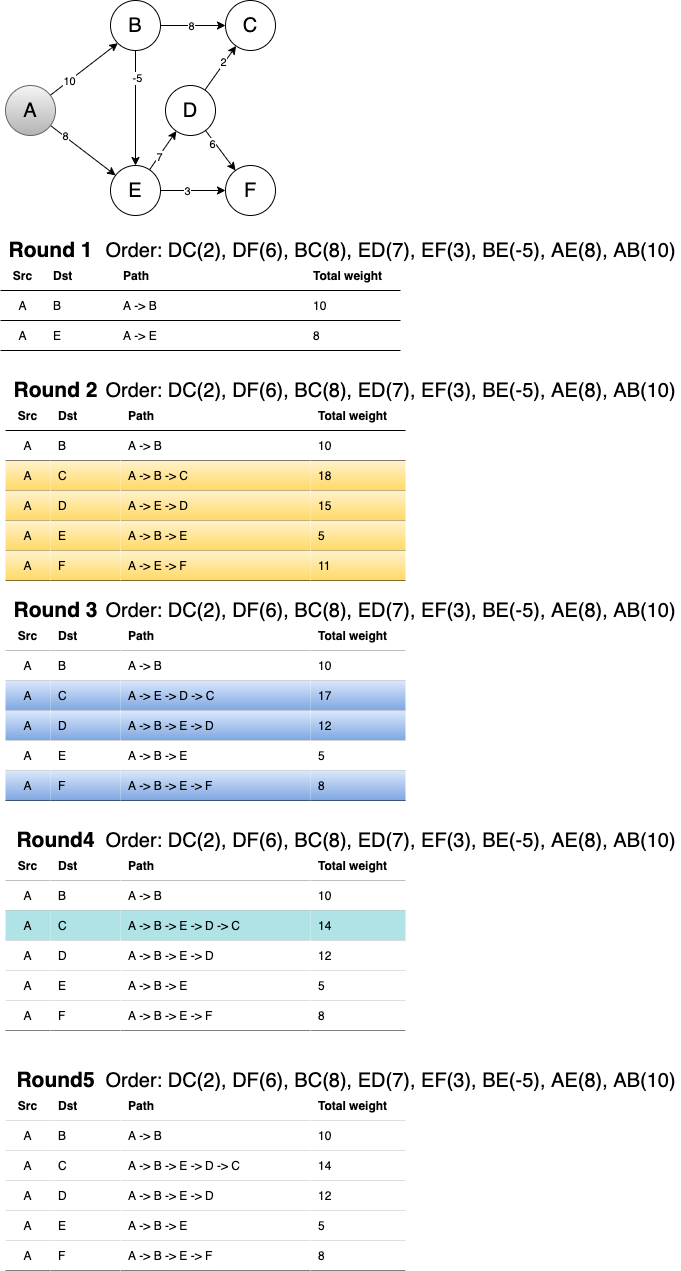
bellman_ford.png

Figure 11: Bellman Ford 算法流程

public Map<V, PathInfo<V>> shortestPathBellmanFord(V source) {
    Vertex<V> sourceVertex = vertices.get(source);
    if (sourceVertex == null) return null;
    Map<Vertex<V>, PathInfo<V>> pathMap = new HashMap<>();

    // init pathMap
    sourceVertex.outEdges.forEach(e -> pathMap.put(e.to, new PathInfo<>(Lists.newArrayList(e.info()), e.weight)));

    for (int i = 0; i < verticesSize() - 1; i++) {
        for (Edge<V> edge : edges) {
            doRelaxation(edge, sourceVertex, pathMap);
        }
    }
    for (Edge<V> edge : edges) { // do one more round
        if (doRelaxation(edge, sourceVertex, pathMap))
            throw new NegativeWeightCycleException();
    }
    pathMap.remove(sourceVertex);
    return pathMap.entrySet().stream()
        .collect(Collectors.toMap(e -> e.getKey().value, e -> e.getValue()));
}

private boolean doRelaxation(Edge<V> edge, Vertex<V> sourceVertex, Map<Vertex<V>, PathInfo<V>> pathMap) {
    //        if (sourceVertex == edge.to) return false;
    //        if (sourceVertex == edge.from) {
    //            PathInfo<V> oldToPathInfo = pathMap.get(edge.to);
    //            if (oldToPathInfo == null) {
    //                pathMap.put(edge.to, new PathInfo<>(Lists.newArrayList(edge.info()), edge.weight));
    //                return false;
    //            } else {
    //                if (edge.weight < oldToPathInfo.weight) {
    //                    oldToPathInfo.weight = edge.weight;
    //                } else {
    //                    return false;
    //                }
    //            }
    //        }
    PathInfo<V> oldFromPathInfo = pathMap.get(edge.from);
    if (oldFromPathInfo == null) return false;
    PathInfo<V> oldToPathInfo = pathMap.get(edge.to);
    PathInfo<V> newToPathInfo = new PathInfo<>();
    newToPathInfo.getEdges().addAll(oldFromPathInfo.getEdges());
    newToPathInfo.getEdges().add(edge.info());
    newToPathInfo.weight = oldFromPathInfo.weight + edge.weight;

    if (oldToPathInfo == null) {
        pathMap.put(edge.to, newToPathInfo);
        return false;
    } else {
        if (oldFromPathInfo.weight + edge.weight < oldToPathInfo.weight) {
            pathMap.put(edge.to, newToPathInfo);
            return true;
        } else {
            return false;
        }
    }
}

6.2.1 负权环检测

如果经历了 V - 1 轮松弛，在第 V 轮松弛后仍然能发现更短的路径，则可以判定图中存在负权环。

负权环指的是遍历一遍环中所有节点，路径权值为负。

6.3 Floyd [O(V3)]

算法思想是，假设 sp(i, j) 为顶点 i 到顶点 j 的当前最短路径，遍历所有顶点 k ，判断 sp(i, k) + sp(k, j) < sp(i, j) 是否成立， 如果成立则更新路径 sp(i, j) = sp(i, k) + sp(k, j) 。

Floyd 算法执行效率优于执行 V 次 Dijkstra 算法。 

public Map<V, Map<V, PathInfo<V>>> shortestPathFloyd() {
    Map<V, Map<V, PathInfo<V>>> pathMap = new HashMap<>();

    // init path map
    vertices.values().forEach(v -> pathMap.put(v.value, new HashMap<>()));
    for (Edge<V> edge : edges) {
        pathMap.get(edge.from.value).put(edge.to.value,
                                         new PathInfo<>(Lists.newArrayList(edge.info()), edge.weight));
    }

    // 须按照 k, i, j 的顺序
    for (Vertex<V> k : vertices.values()) {
        for (Vertex<V> i : vertices.values()) {
            for (Vertex<V> j : vertices.values()) {
                if (j == k || j == i || k == i) continue;

                PathInfo<V> pathInfoIK = pathMap.get(i.value).get(k.value);
                if (pathInfoIK == null) continue;
                PathInfo<V> pathInfoKJ = pathMap.get(k.value).get(j.value);
                if (pathInfoKJ == null) continue;
                PathInfo<V> pathInfoIJ = pathMap.get(i.value).get(j.value);
                if (pathInfoIJ == null || pathInfoIK.weight + pathInfoKJ.weight < pathInfoIJ.weight) {
                    PathInfo<V> newPathInfoIJ = new PathInfo<>();
                    newPathInfoIJ.edges = Lists.newArrayList(pathInfoIK.getEdges());
                    newPathInfoIJ.edges.addAll(pathInfoKJ.edges);
                    newPathInfoIJ.weight = pathInfoIK.weight + pathInfoKJ.weight;
                    pathMap.get(i.value).put(j.value, newPathInfoIJ);
                }
            }
        }
    }
    return pathMap;
}

Footnotes:

1

并查集

Author: Hao Ruan (ruanhao1116@gmail.com)

Created: 2021-02-12 Fri 16:37

Updated: 2021-08-17 Tue 11:23

Emacs 27.1 (Org mode 9.3)