字符串匹配算法
{Back to Index}
Table of Contents
1 暴力匹配(BF) [\(O(nm)\)]
1.1 解法思路
使用 \(pi \in [0, plen)\) 和 \(ti \in [0, tlen)\) 分别表示模式字符串和文本字符串参与比较的索引位置。
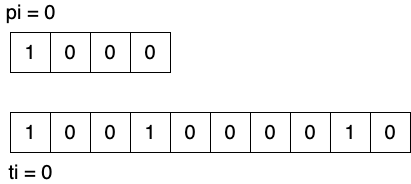
Figure 1: 定义两个索引变量
1.1.1 对应位置匹配成功
当 \(p[pi] == t[ti]\) ,则执行 \(pi++\) 和 \(ti++\) 。
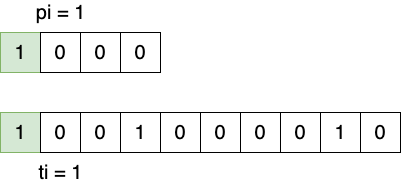
Figure 2: 字符匹配成功
1.1.2 对应位置匹配失败
当 \(p[pi] \ne t[ti]\) ,则执行 \(pi = 0\) 和 \(ti = (ti - pi + 1)\) 。 其中 \(ti - pi\) 代表 \(ti\) 回到 一开始比较的位置 , \(+1\) 即表示向后移一位,即 新的比较起点 。
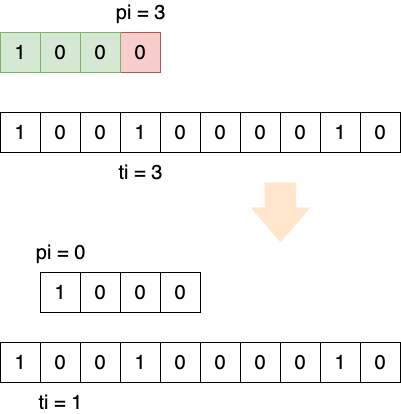
Figure 3: 字符匹配失败
1.1.3 完全匹配成功条件
当 \(pi == plen\) 表示匹配成功,而返回的索引位置为 \(ti - pi\) 。
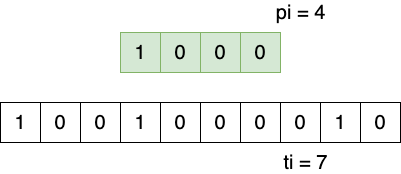
Figure 4: 串匹配成功
1.2 代码实现
public int bf_match(String text) { int pi = 0; int ti = 0; char[] t = text.toCharArray(); while (ti < t.length) { if (p[pi] == t[ti]) { pi++; ti++; if (pi == p.length) return ti - pi; } else { ti = (ti - pi + 1); pi = 0; } } return -1; }
1.3 优化思路
通过选择恰当的时机 提前退出 ,来减少比较次数,从而达到优化的目的。
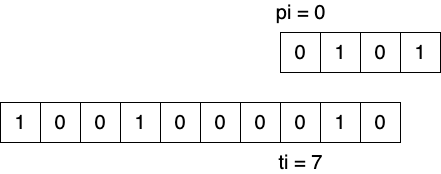
Figure 5: 可提前退出的场景
public int bf_optimized_match(String text) { int pi = 0; int ti = 0; char[] t = text.toCharArray(); while (ti < t.length) { if (p[pi] == t[ti]) { pi++; ti++; if (pi == p.length) return ti - pi; } else { ti = (ti - pi + 1); pi = 0; if (ti > t.length - p.length) return -1; // 提前退出 } } return -1; }
2 KMP [\(O(n+m) \sim O(2n+m)\)]
2.1 算法特点
相比暴力匹配,KMP 算法利用了模式串自身的特点(有公共前后缀), 跳过没必要比较的位置 ,从而实现快速匹配的目的。
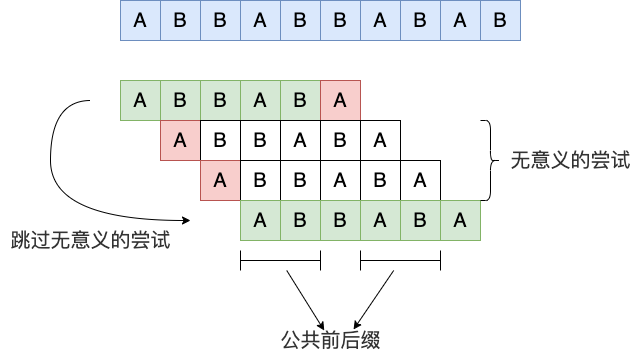
Figure 6: KMP 算法特点
2.2 next 表
KMP 会预先根据模式串的内容生成 next 数组,下图展示了模式串为 \(ABCDABCE\) 所对应的 next 数组:
\begin{array}{r|rrrrrrrr} pattern & A & B & C & D & A & B & C & E & \\ \hline idx & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & \\ next[idx] & 0 & 0 & 0 & 0 & 0 & 1 & 2 & 3 & \\ \end{array}
使用 next 表的 意义 在于当 \(pi\) 和 \(ti\) 位置上的字符不匹配时,直接将 \(pi\) 赋值为 \(nenxt[pi]\) ,并 继续 匹配。
中间会 跳过 \(pi - next[pi]\) 个位置,而这些位置 其实 都是无效的尝试。
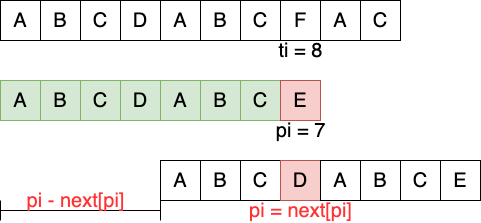
Figure 7: 匹配失败时,通过 next 表快速推进
\(next[pi]\) 的值的含义是:\(pi\) 位置(不包含) 左边子串的最大公共前后缀长度 。
2.2.1 next 表构建
构建 next 数组,是 KMP 算法的 精髓 ,这篇文章1解释了计算 next 数组的原理与思路, 但是对算法的描述感觉像是动态规划,但我觉得更应该是一种回溯,以下是我对算法的理解:
使用 \(next[i]\) 表示 \(p[0] \sim p[i]\) 这一段字符中真前缀和真后缀的 最大公共子串长度 ,
其中 \(i \in [1, p.length)\) , 并将 \(next[0]\) 初始化为 0 。
字符串的真前缀和真后缀,指的是不包含完整串的前缀和后缀,以字符串 thank 为例: 前缀: t, th, tha, than, thank 真前缀: t, th, tha, than 后缀: thank, hank, ank, nk, k 真后缀: hank, ank, nk, k
同时使用 \(j\) 来表示 每次 对 \(i\) 的迭代中,求得的 真前缀最后一个字符的索引 , \(j\) 最终值的确定需要利用回溯(\(j = next[j-1]\)), 并在下一次迭代前递增,其实整个算法的难点就在于如何通过回溯求得 \(j\) ,下图是针对这一计算过程的简单示例:

Figure 8: \(i\) 和 \(j\) 迭代的过程
将数组整体右移一位,即得到了上一节所讨论的更便于计算的 next 数组:
int[] buildNextArrayShift() { int[] next = new int[p.length]; next[0] = 0; int j = 0; for (int i = 1; i < p.length; i++) { while (j >= 1 && p[j] != p[i]) { j = next[j - 1]; } if (p[j] == p[i]) { // next[i] = ++j; next[i+1] = ++j; // 这种做法效果是所有值向右移动一位 } } return next; }
2.2.2 next 表优化
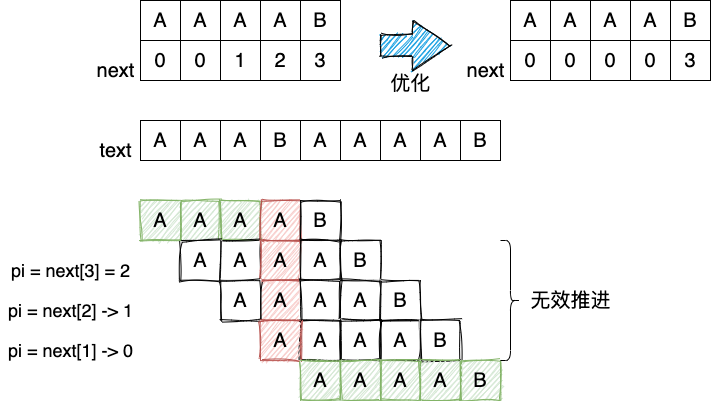
Figure 9: 优化 next 数组
int[] buildNextArrayShiftOptimized() { int[] next = new int[p.length]; next[0] = 0; int j = 0; for (int i = 1; i < p.length; i++) { while (j >= 1 && p[j] != p[i]) { j = next[j - 1]; } if (p[j] == p[i]) { next[i + 1] = ++j; if (p[i + 1] == p[next[j]]) { next[i + 1] = next[j]; // optimize } } } return next; }
2.3 代码实现
public int kmp_match(String text) { int[] next = buildNextArrayShift(); int pi = 0; int ti = 0; char[] t = text.toCharArray(); while (ti < t.length) { if (p[pi] == t[ti]) { pi++; ti++; if (pi == p.length) return ti - pi; } else { // not match if (pi == 0) ti++; // 当 pi 不能再回溯了,只有 ti++ pi = next[pi]; if (ti > t.length - p.length) return -1; } } return -1; }
3 其他算法
3.1 Boyer-Moore [\(O(\frac{n}{m}) \sim O(n+m)\)]
该算法的特点是从模式串的 尾部 开始匹配,且有一个 坏字符表 和一个 好后缀表 。
3.2 Sunday
思想与 Boyer-Moore 算法类似,不同的是从前向后匹配。
3.3 Rabin-Karp
基于 哈希 的字符串匹配算法,基本思想为将模式串的哈希值与文本串中每个子串的哈希值进行比较。