映射型数据结构
{Back to Index}

1. HashMap
2. LinkedHashMap
- 2.1. 添加节点时维护顺序
- 2.2. 删除节点时维护顺序
  - 2.2.1. 可以直接删除的情况
  - 2.2.2. 删除的是前驱/后继节点的情况
3. 跳表

1 HashMap

1.1 JDK HashMap 实现方案

JDK 的哈希表是使用 单向链表和红黑树 来实现的。

默认使用单向链表将同一个桶中的元素连接起来。

在添加元素时，可能会由单向链表 转为红黑树 来存储元素，转换的条件是当桶的数量 大于等于 64 且单向链表的节点数量 大于等于 8 。

当红黑树节点数量减少到一定程度(\(\le 6\))，又会转为单向链表形式。

1.2 \(hashcode\) 和 \(equals\)

使用自定义对象作为 key ，需要同时重写 \(hashCode\) 和 \(equals\) 方法。

\(equals\) 方法作用是判断 2 个 key 是否为 同一个 ， \(hashCode\) 方法是为 key 选择桶的位置，必须保证 \(equals\) 为 true 的 2 个 key 的哈希值是一样的，反过来，哈希值相等的 key ，不一定相同。

如果不重写 \(hashCode\) 而 只重写 \(equals\) 会导致 2 个 \(equals\) 为 true 的 key 同时存在于哈希表中。

1.3 插入操作(put)

HashMap 并没有强制要求键值需要具备可比较性 ，对于 \(put(key, value)\) 操作，并假设桶内存放的是已是红黑树节点，则确定新插入节点最终存放位置的逻辑大致为：

先根据 key 的哈希值大小进行二分查找
如哈希值相同则通过 \(equals\) 方法检查是否为相同的 key
如果不是相同的 key ，则检查 key 是否具备可比较行(是否实现 Comparable 接口)，并根据 \(compareTo\) 方法的返回值继续二分搜索。
这里 不考虑 \(compareTo\) 返回值为 0 的情况，因为 \(a.compareTo(b) == 0\) 并不意味 \(a.equals(b) == true\) 。
如仍无法比较大小，则必须对左右子树进行遍历以确定是否已存在该节点
如子树中不存在该节点，则以内存地址大小 (\(System.identityHash()\)) 为比较条件来确定最终需要插入节点的位置

2 LinkedHashMap

在 HashMap 的基础上 维护元素的添加顺序 ，使得遍历结果遵从添加顺序。

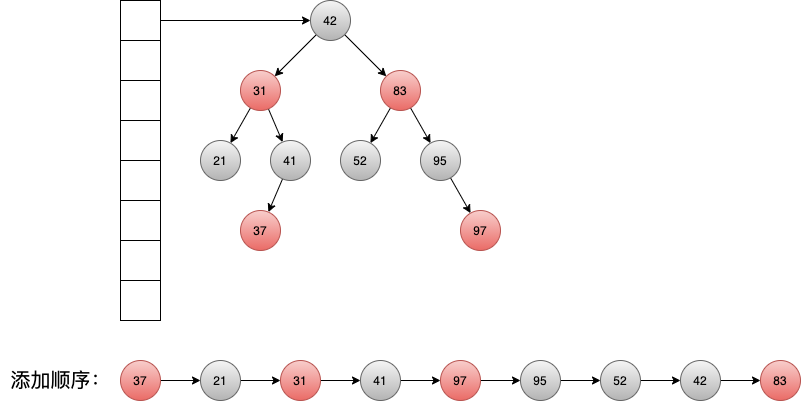
Figure 1: 通过链表结构维护添加顺序

2.1 添加节点时维护顺序

添加节点时维护添加顺序比较直观，只需要更新尾节点的指针即可。

2.2 删除节点时维护顺序

2.2.1 可以直接删除的情况

如果节点 可以直接删除 ，比如红色节点，则更新前后节点相应的指针即可，如：

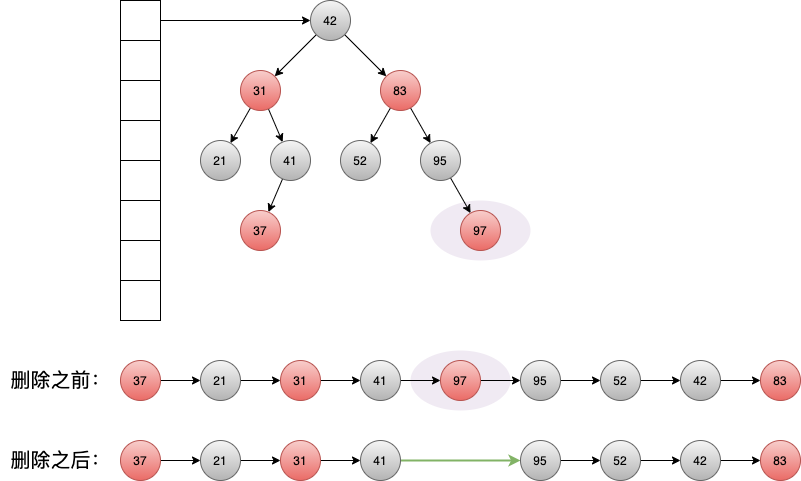
Figure 2: 被删节点为红色节点，直接删除，并更新链表指针

2.2.2 删除的是前驱/后继节点的情况

如果删除的是 度为 2 的节点，因为此时真正被删除的是前驱或者后继节点，因此需要特殊处理，即 更换节点与前驱或后继节点在链表中的位置 ：

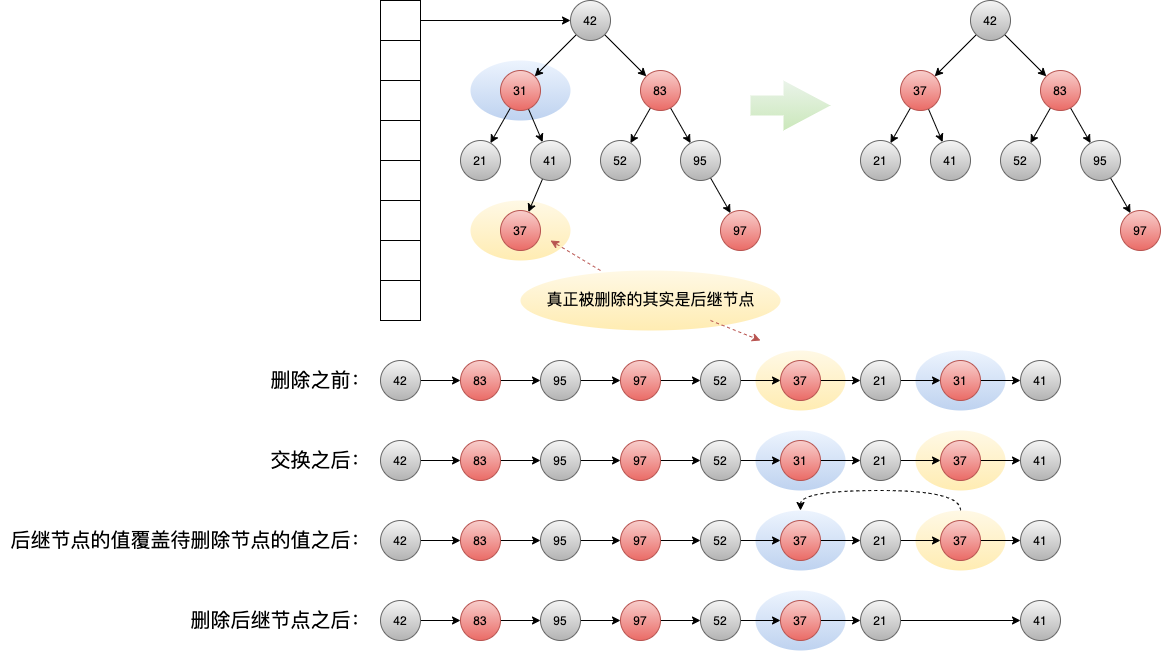
Figure 3: 需要删除的节点 并非真正删除的节点 的情况

3 跳表

通常，有序链表的搜索，添加，删除操作的平均时间复杂度为 \(O(n)\) ，跳表可以将这些操作的复杂度优化到 \(O(logn)\) 。

由于跳表的实现与维护相对简单，因此 跳表设计的初衷是为了取代平衡树 。

跳表通常用于存放键值对，作用和 TreeMap 类似。

跳表的最底层可以看成是 原始数据 ，而其他层可以看作索引。

Redis 的 SortedSet 底层是使用跳表实现的。

3.1 搜索操作

从顶层链表的首元素开始，从左往右搜索，直至找到一个大于或等于目标的元素，或者到达当前层链表的尾部
如果该元素等于目标元素，则表明该元素已被找到
如果该元素大于目标元素或已到达链表的尾部，则退回到当前层的前一个元素，然后转入下一层进行搜索

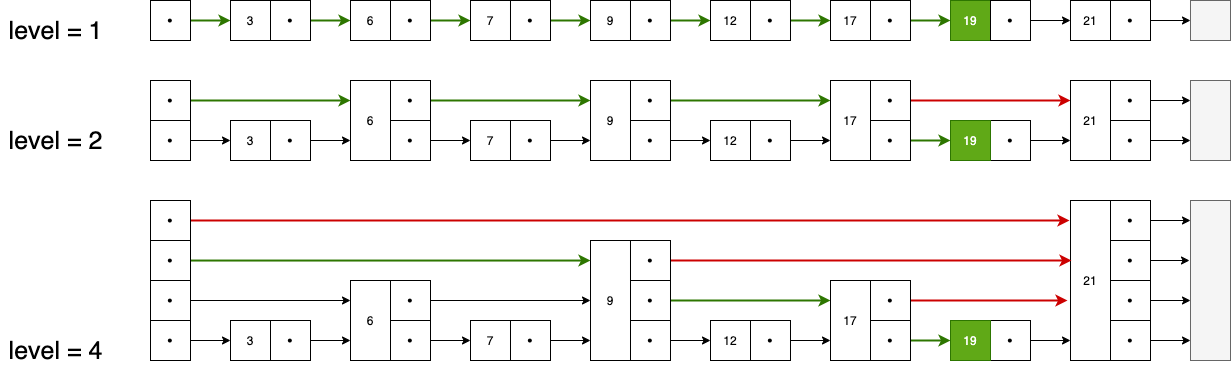
Figure 4: 搜索 key==19 示意图

搜索操作代码示例:

public V get(@NonNull K key) {
    Node<K, V> node = head;
    for (int i = level - 1; i >= 0; i--) { // 从顶层到底层，遍历头节点的 nexts 指针数组
        int cmp = -1;
        while (node.nexts[i] != null &&
               (cmp = compare(node.nexts[i].key, key)) < 0) {
            node = node.nexts[i];
        }
        // 到这里说明 node.nexts[i].key >= key
        if (cmp == 0) return node.nexts[i].value;
    }
    return null;
}

3.2 添加操作

3.2.1 确定节点层数

每个节点的层数是 随机确定 的，通过数学统计已经证明了此种做法依然可以保证预期的时间复杂度。 😲

Redis 中计算层数的思路也是类似的：

private int randomLevel() {
    int level = 1;
    while (Math.random() < P && level < MAX_LEVEL) level++;
    return level;
}

跳表中元素的平均层数是 \(\frac{1}{1-p}\) ，因此当 \(p = \frac{1}{2}\) 时，平均层数是 2 ；当 \(p = \frac{1}{4}\) 时，平均层数是 1.33 ，层数即为 nexts 数组长度。

考虑到二叉树每个节点要保存父子节点 3 个指针，因此跳表相比二叉树要 节省内存 。

3.2.2 查找添加位置

添加操作的本质是查找需要被添加的位置，并更新前驱节点(即 \(6, 9, 12\))的指针和指向后继节点(即 \(19, 21\))的指针。

添加操作的难点在于如何确定前驱节点对应层数的 next 指针，即图中待插入节点前面彩色的部分。彩色指针的特点为它们指向的节点必定 \(\ge\) 待添加节点或指向 null 。

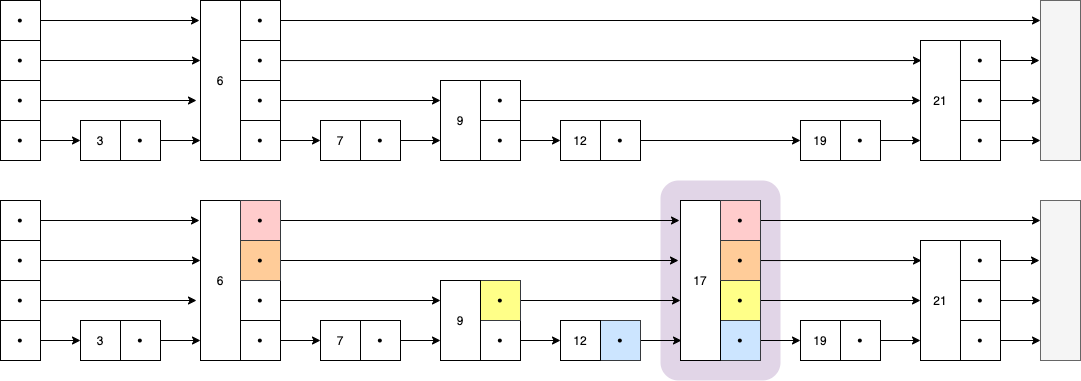
Figure 5: 添加一个节点(彩色部分是 需要更新的指针)

public V put(@NonNull K key, V value) {
    Node<K, V> node = head;
    Node[] prevs = new Node[level]; // 记录每一层对应的前驱节点
    for (int i = level - 1; i >= 0; i--) { // 从顶层到底层，遍历头节点的 nexts 指针数组
        int cmp = -1;
        while (node.nexts[i] != null &&
               (cmp = compare(node.nexts[i].key, key)) < 0) {
            node = node.nexts[i];
        }
        if (cmp == 0) {  // already exists, just update value
            Node<K, V> old = node.nexts[i];
            old.value = value;
            return old.value;
        }
        prevs[i] = node;
    }
    // 到这里说明需要添加一个全新的节点
    int newNodeLevel = randomLevel();
    Node<K, V> newNode = new Node<>(key, value, newNodeLevel);
    for (int i = 0; i < newNodeLevel; i++) {
        if (i >= level) { // 新节点层数高于跳表有效层数
            head.nexts[i] = newNode; // 直接将首节点对应层数中的 next 指针指向新节点即可
            continue;
        }
        newNode.nexts[i] = prevs[i].nexts[i];
        prevs[i].nexts[i] = newNode;
    }
    level = Math.max(level, newNodeLevel);
    size++;
    return null;
}

3.3 删除操作

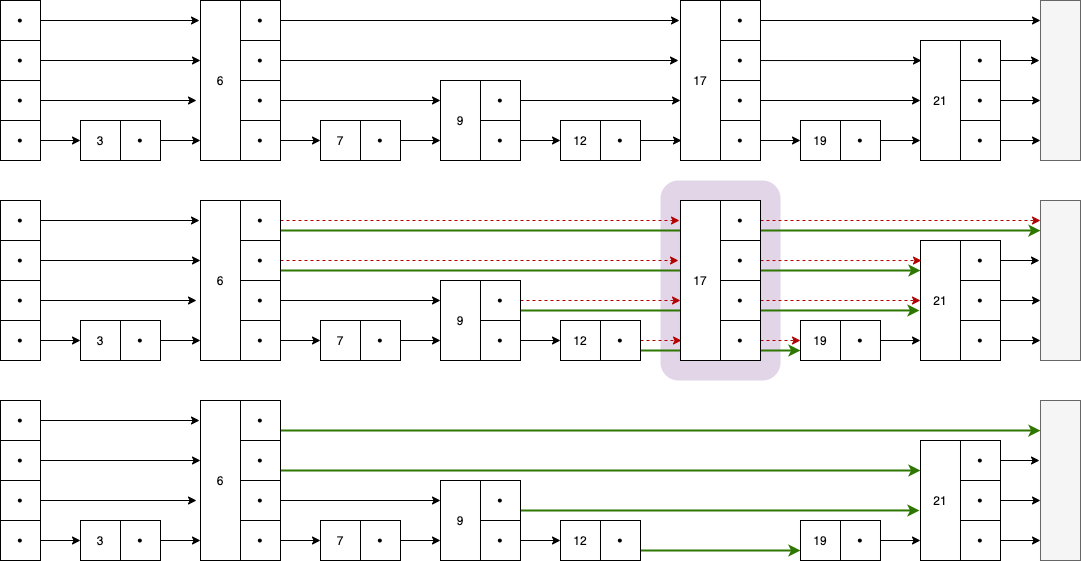
Figure 6: 删除节点时需要将前驱节点的指针更新为后继节点

public V remove(@NonNull K key) {
    Node<K, V> node = head;
    Node[] prevs = new Node[level]; // 记录每一层对应的前驱节点
    boolean exist = false;
    for (int i = level - 1; i >= 0; i--) { // 从顶层到底层，遍历头节点的 nexts 指针数组
        int cmp = -1;
        while (node.nexts[i] != null &&
               (cmp = compare(node.nexts[i].key, key)) < 0) {
            node = node.nexts[i];
        }
        // 就算找到要删除的节点，遍历也要继续，因为要找到所有的前驱节点
        // 这里要做的只是记录下被删节点是否存在
        if (cmp == 0) exist = true;
        prevs[i] = node;
    }
    if (!exist) return null;
    Node<K, V> nodeToRemove = node.nexts[0]; // node.nexts[0] 必然是被删节点

    for (int i = 0; i < nodeToRemove.nexts.length; i++) {
        prevs[i].nexts[i] = nodeToRemove.nexts[i];
    }
    size++;
    // 更新跳表有效层数
    for (int i = level; i >= 0; i--) {
        if (head.nexts[i - 1] != null) {
            level = i;
            break;
        }
    }
    return nodeToRemove.value;
}

映射型数据结构 {Back to Index} Expand All Details on Page

Table of Contents