排序算法
{Back to Index}

1. 时间复杂度递推公式
2. 基于比较的排序算法
3. 基于空间换时间的排序算法
4. 性能对比

1 时间复杂度递推公式

递推式	时间复杂度
\(T(n) = T(\frac{n}{2}) + O(1)\)	\(O(logn)\)
\(T(n) = T(\frac{n}{2}) + O(n)\)	\(O(n)\)
\(T(n) = 2* T(\frac{n}{2}) + O(1)\)	\(O(n)\)
\(T(n) = 2* T(\frac{n}{2}) + O(n)\)	\(O(nlogn)\)
\(T(n) = T(n - 1) + O(1)\)	\(O(n)\)
\(T(n) = T(n - 1) + O(n)\)	\(O(n^2)\)
\(T(n) = 2 * T(n - 1) + O(1)\)	\(O(2^n)\)
\(T(n) = 2 * T(n - 1) + O(n)\)	\(O(2^n)\)

2 基于比较的排序算法

2.1 冒泡排序

2.1.1 排序思路

从头部开始比较每一对 相邻元素 ，如左边大于右边，则交换位置。每执行完一轮，尾部元素即为此轮的最大值。

2.1.2 代码实现

protected void sort() {
    for (int end = array.length - 1; end >= 1; end--) {
        for (int begin = 1; begin <= end; begin++) {
            // E left = array[begin-1];
            // E right = array[begin];
            if (compare(begin-1).gt(begin)) {
                swap(begin-1, begin);
                // array[begin-1] = right;
                // array[begin] = left;
            }
        }
    }
}

2.1.3 优化方案1(提前退出)

假设某一轮冒泡操作后，发现没有执行过交换操作，表明整个序列已是有序状态，无需继续剩余轮次的冒泡操作。

此优化方案对性能提高不明显 ，因为前提是数组能在某一轮次中呈现有序性，而这种情况出现概率较小。

protected void sort() {
    for (int end = array.length - 1; end >= 1; end--) {
        boolean sorted = true;
        for (int begin = 1; begin <= end; begin++) {
            if (compare(begin - 1).gt(begin)) {
                swap(begin - 1, begin);
                sorted = false;
            }
        }
        if (sorted) {
            return; // 数组已经有序，提前结束
        }
    }
}

2.1.4 优化方案2(减少比较次数)

如果序列尾部已经局部有序，可以记录最后一次交换位置，从而减少比较次数。

protected void sort() {
    for (int end = array.length - 1; end >= 1; end--) {
        int lastSwapIndex = 1; // 初始值设为 1 的意义在于如果序列完全有序，则可以提前终止排序
        for (int begin = 1; begin <= end; begin++) {
            if (compare(begin - 1).gt(begin)) {
                swap(begin - 1, begin);
                lastSwapIndex = begin;
            }
        }
        end = lastSwapIndex;
    }
}

2.2 选择排序

2.2.1 排序思路

从序列中找出最大的元素，与最末尾的元素交换位置。

2.2.2 代码实现

protected void sort() {
    for (int end = array.length - 1; end >= 1; end--) {
        int maxIndex = 0;
        for (int begin = 0; begin <= end; begin++) {
            if (compare(begin).gt(maxIndex)) maxIndex = begin;
        }
        swap(end, maxIndex);
    }
}

2.2.3 支持稳定性的解法

protected void sort() {
    for (int end = array.length - 1; end >= 1; end--) {
        int maxIndex = 0;
        for (int begin = 0; begin <= end; begin++) {
            if (compare(begin).ge(maxIndex)) maxIndex = begin; // 改为 >= 即可
        }
        swap(end, maxIndex);
    }
}

2.3 堆排序

2.3.1 排序思路

堆排序其实是对选择排序的一种优化方案。 即把选择最大值这个操作交由堆来处理。

首先对序列原地建堆（大顶堆），即将原序列变为堆序列
重复一下操作，直至堆元素数量为 1
- 交换堆顶元素与尾元素
- 堆元素数量减1
- 对0位置进行 siftDown 操作

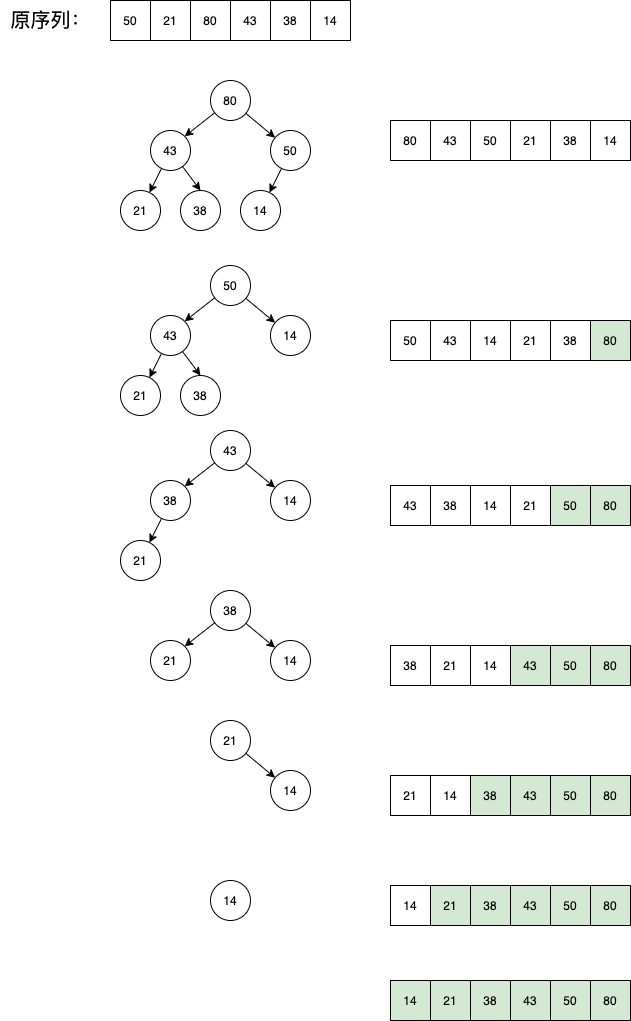
Figure 1: 堆排序过程

2.3.2 代码实现

protected void sort() {
    size = array.length;
    heapify();
    for (; size > 1;) {
        swap(0, --size);
        siftDown(0);
    }
}

2.4 插入排序

2.4.1 排序思路

在执行过程中，会将序列分为 2部分 : 头部是已排好序的，尾部是待排序的。
插入指的是从尾部取出一个元素，并从头部依次扫描，当找到合适位置，就插入，插入后头部仍然是有序的。

2.4.2 代码实现(交换)

protected void sort() {
    for (int i = 1; i < array.length; i++) {
        for (int j = i; j > 0 ; j--) {
            if (compare(j-1).gt(j)) {
                swap(j-1, j);
            } else {
                break; // 说明头部已经是有序的
            }
        }
    }
}

2.4.3 优化方案(挪动)

先将待插入元素备份
头部中所有比插入元素大的，都朝尾部移动 一个位置
将待插入元素放到合适位置

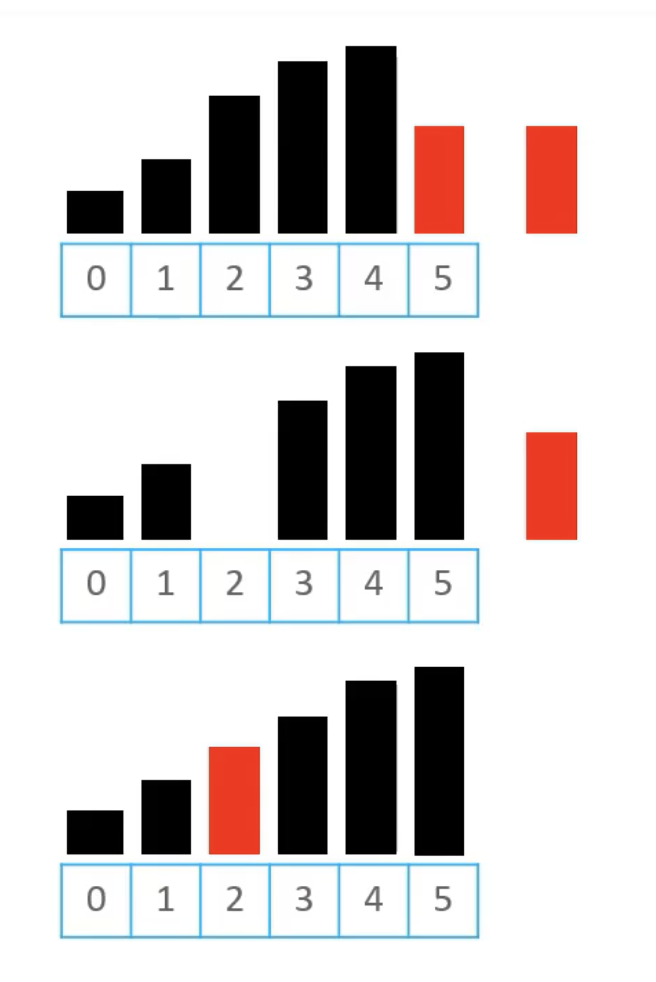
Figure 3: 挪动方案示意图

protected void sort() {
    for (int i = 1; i < array.length; i++) {
        E v = array[i];
        int pos = i;
        for (int j = i; j > 0 ; j--) {
            if (compare(array[j - 1]).gt(v)) {
                pos = j - 1;
                array[pos + 1] = array[pos]; // 挪动
            } else {
                break; // 说明头部已经是有序的
            }
        }
        array[pos] = v; // 插入
    }
}

2.4.4 优化方案(使用二分搜索)

使用二分搜索法来确定新元素应该放在已排序数列的位置。该优化方案的思想是减少比较的次数，但是由于数据搬运仍然是不可避免的，因此时间负责度依旧是 \(O(n^2)\) 。

@Override
protected void sort() {
    for (int i = 1; i < array.length; i++) {
        insert(i, search(i));
    }
}

// length 既是左边已排好序的序列长度，也是右边未排序序列的第一个元素索引
// 查找 v 在有序部分中的插入位置，这个位置其实是"第一个大于 v 的元素"的索引
// 已排好序的数据范围是 [0, length)
private int search(int length) {
    E v = array[length];
    int begin = 0;
    int end = begin + length;
    while (begin != end) {
        int middle = (begin + end) / 2;
        if (compare(v).ge(array[middle])) {
            begin = middle + 1;
        } else {
            end = middle;
        }
    }
    return begin;
}


// 将 sourceIndex 位置的元素插入到 pos 位置
private void insert(int sourceIndex, int pos) {
    E v = array[sourceIndex];
    for (int j = sourceIndex; j > pos; j--) { // 整体向右移动一个位置
        array[j] = array[j - 1];
    }
    array[pos] = v;
}

2.5 归并排序 [\(O(nlogn)\)]

2.5.1 排序思路

不断将序列平均分割成两个子序列，直至分割到只剩一个元素
不断将两个子序列合并成一个序列

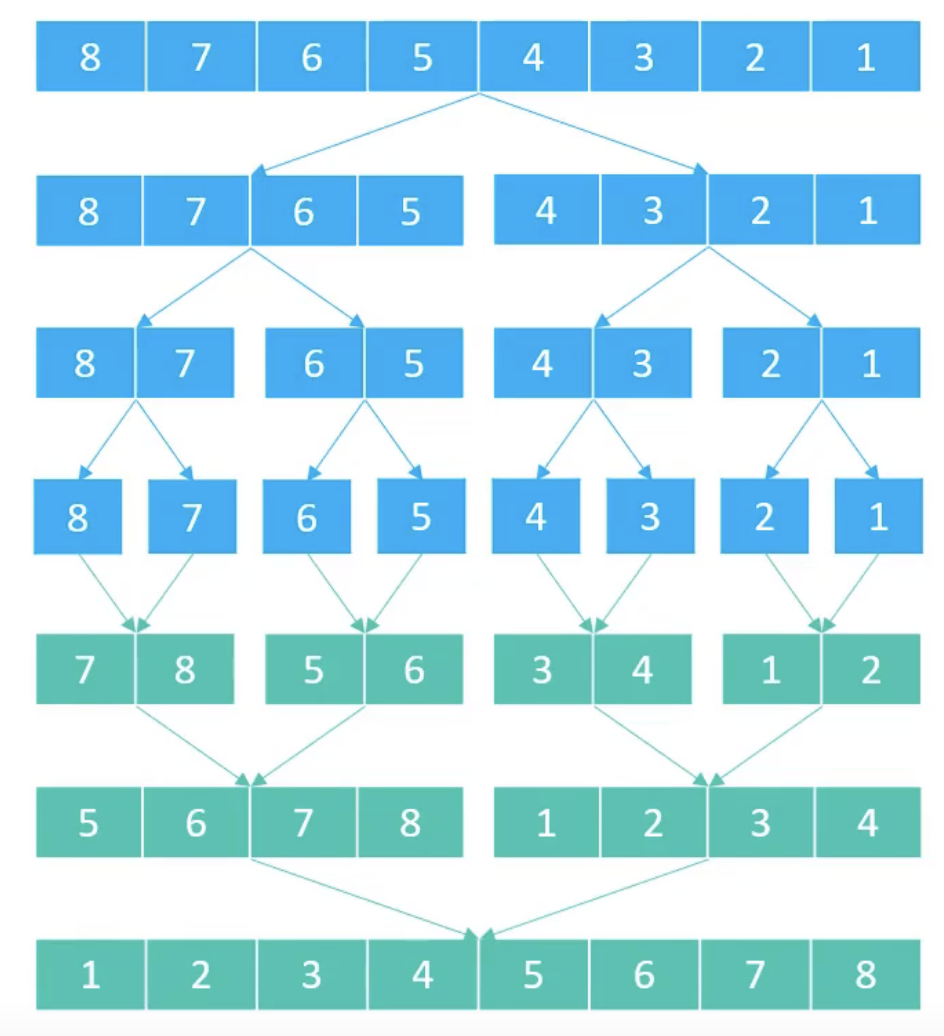
Figure 4: 算法流程

2.5.1.1 merge 细节

因为 merge 不能原地操作，可以备份左边数组作为中间存储区域。

2.5.2 代码实现

private E[] leftBackup; // 共用的中间存储区域

// 对 [begin, end) 范围内的元素进行排序
private void sort(int begin, int end) {
    int numberOfElements = end - begin;
    if (numberOfElements < 2) return;

    int mid = (begin + end) / 2;
    sort(begin, mid);
    sort(mid, end);
    merge(begin, mid, end);
}

// 对 [begin, mid) 和 [mid, end) 两部分数据进行归并
private void merge(int begin, int mid, int end) {
    int li = 0, le = mid - begin; // 左边数组(leftBackup)的起始索引和结束索引(不包含)
    int ri = mid, re = end; // 右边数组的起始索引和结束索引(不包含)
    int ai = begin; // 最终数据存放的起始索引

    for (int i = 0; i < le; i++) {
        leftBackup[i] = array[begin + i]; // 对左边元素进行备份
    }

    while (li < le && ri < re) {
        if (compare(leftBackup[li]).le(array[ri])) {
            array[ai++] = leftBackup[li++];
        } else {
            array[ai++] = array[ri++];
        }
    }

    while (li < le) {
        array[ai++] = leftBackup[li++];
    }

}

@Override
protected void sort() {
    leftBackup = (E[]) new Comparable[array.length / 2];
    sort(0, array.length);
}

2.6 快速排序

2.6.1 排序思路

快速排序的基本思想是： 逐渐将每一个元素都转换成轴点元素 。

从序列中选择一个轴点元素 (pivot) 假设每次选择 0 位置的元素为轴点元素
利用 pivot 将序列分割成 2 个子序列
- 将小于 pivot 的元素放在pivot前面（左侧）
- 将大于 pivot 的元素放在pivot后面（右侧）
- 等于pivot的元素放哪边都可以
对子序列递归地进行上述2步操作，直到不能再分割（子序列中只剩下1个元素）

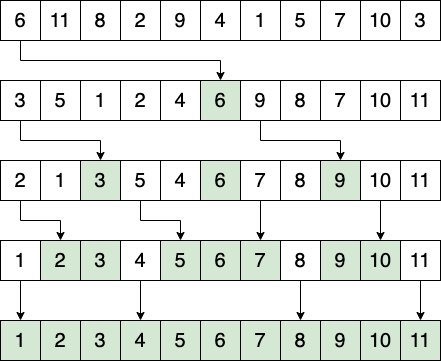
Figure 5: 快速排序过程

2.6.2 轴点位置的确定

将 0 位置的元素备份，并作为轴点元素。

轴点最终位置的选择需要先从右往左找，找到以后再从左往右，不断循环这个过程，直到把所有比轴点元素小的元素放到左半部分，把所有比轴点元素大的元素放到右半部分，假设 begin 表示序列首位置，此过程的逻辑可以描述为：

从右往左扫描，寻找比轴点元素小的元素找到以后，放到 begin 位置， \(begin++\) ，然后 反向寻找
从左往右扫描，寻找比轴点元素大的元素找到以后，放到 end 位置， \(end--\) ，然后 反向寻找
当 \(begin == end\) ，说明左右都扫描完了，begin(或 end) 就是轴点的最终位置，此时可以将一开始备份的轴点元素放到此位置

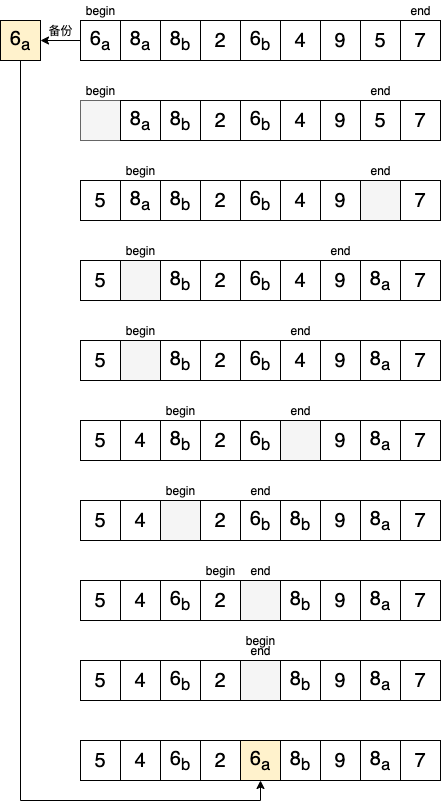
Figure 6: 过程的本质是用轴点元素不断的 比较与交换 ，而备份，只是为了 减少交换次数所做的优化

2.6.3 代码实现

@Override
protected void sort() {
    doSort(0, array.length);
}

// [begin, end)
private void doSort(int begin, int end) {
    if ((end - begin) < 2) return;
    int pivotIndex = quickSort(begin, end);
    doSort(begin, pivotIndex);
    doSort(pivotIndex + 1, end);
}

/**
 * search through [begin, end)
 *
 * @return the index where the pivot should be at
 */
private int quickSort(int begin, int end) {
    end--; // 先减一，不然会越界
    E pivot = array[begin];
    while (begin != end) {
        // 右到左
        while (begin != end) {
            if (compare(array[end]).lt(pivot)) {
                array[begin++] = array[end];
                break;
            } else {
                end--;
            }
        }

        // 左到右
        while (begin != end) {
            if (compare(begin).gt(pivot)) {
                array[end--] = array[begin];
                break;
            } else {
                begin++;
            }
        }
    }
    array[begin] = pivot;
    return begin;
}

代码中嵌套在外层 while 内的 2 个内层 while ，这种写法 值得玩味 。

2.6.4 优化方案(随机交换元素)

在轴点最终确定位置左右元素数量比较均匀的情况下，时间复杂度较好，最好情况可以是 \(O(nlogn)\) 。

但是如果左右元素数量极度不均匀，可能出现最坏情况，这时的复杂度会退化为 \(O(n^2)\) 。

为了降低最坏情况的出现概率，一般采取的做法是： 随机选择轴点元素 ，即在备份轴点元素前，将 begin 位置的元素与序列中的 随机位置元素交换一下 。

private int quickSort(int begin, int end) {
    ...

    swap(begin, begin + (int) (Math.random() * (end - begin))); // 随机交换

    ...
}

2.7 希尔排序

2.7.1 排序思路

希尔排序把序列看作是一个矩阵，分成 m 列，逐列进行排序:

n 从某个整数逐渐减为 1
当 m 为1时，整个序列将完全有序

列数取决于步长序列，例如 {1, 8, 16} 代表依次分成 16 列，8 列，1 列，并逐列排序。（不同步长序列的选择，其执行效率也不同）

2.7.1.1 看图举例 ¹

假设有如下序列： { 16, 15, 14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1 } 且步长序列是 { 1, 2, 4, 8 } 。

Figure 7: 原始序列

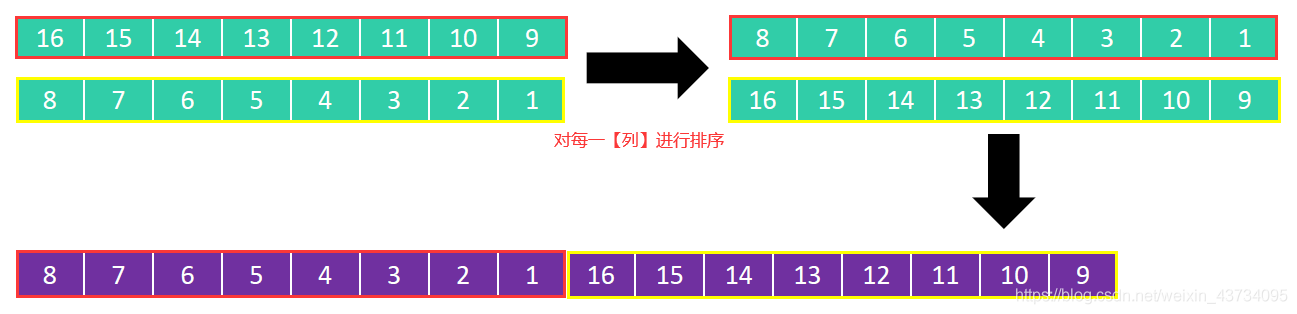
Figure 8: 首先分为 8 列，对每一列进行排序

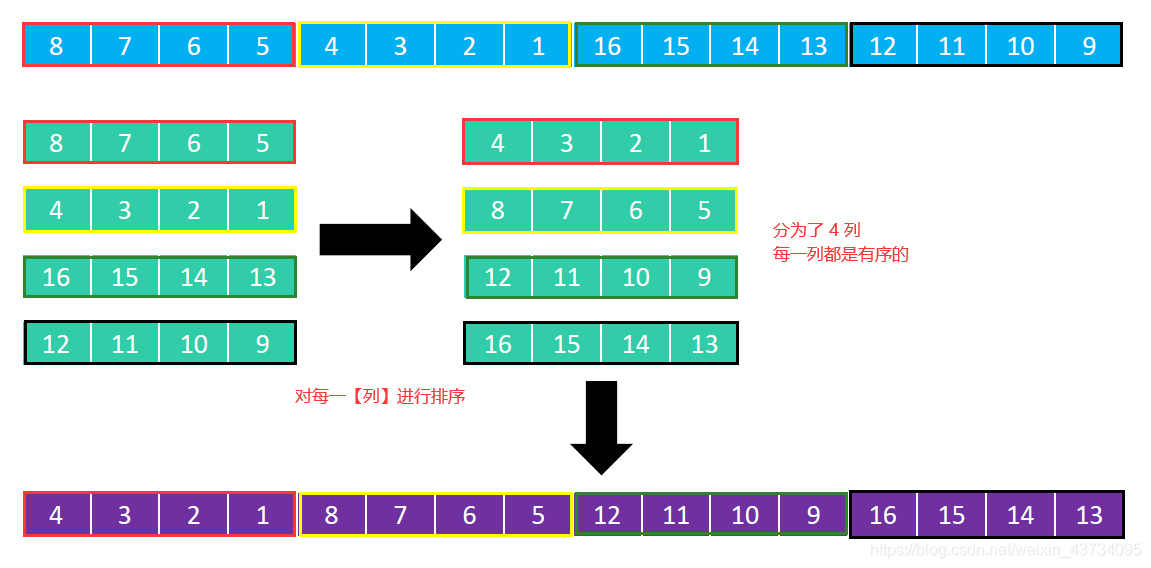
Figure 9: 然后分为 4 列，对每一列进行排序

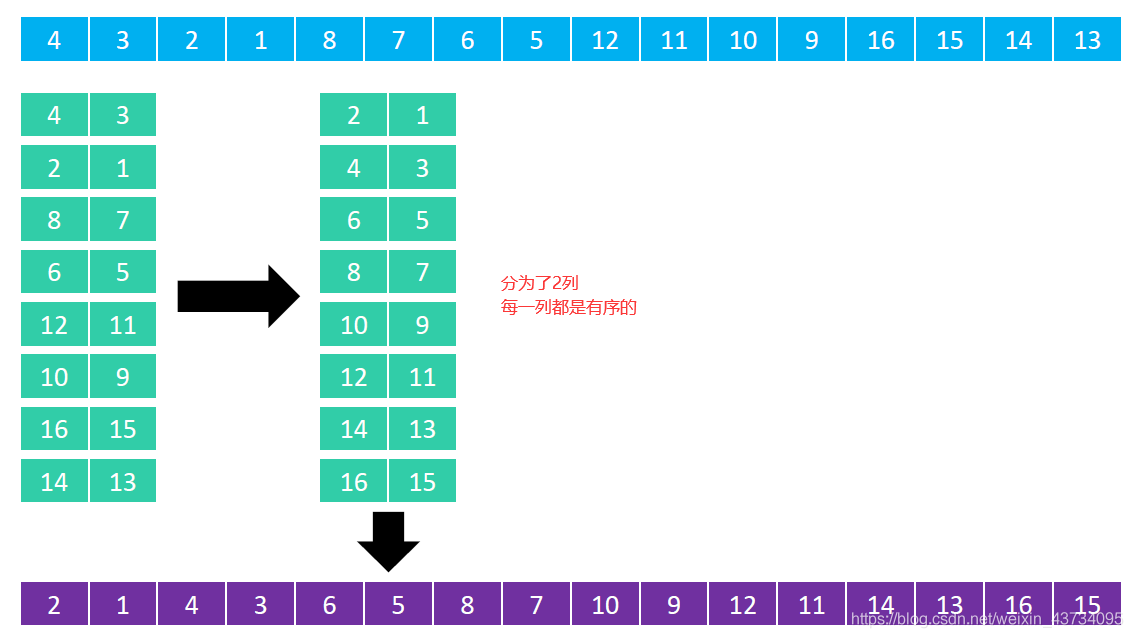
Figure 10: 然后分为 2 列，对每一列进行排序

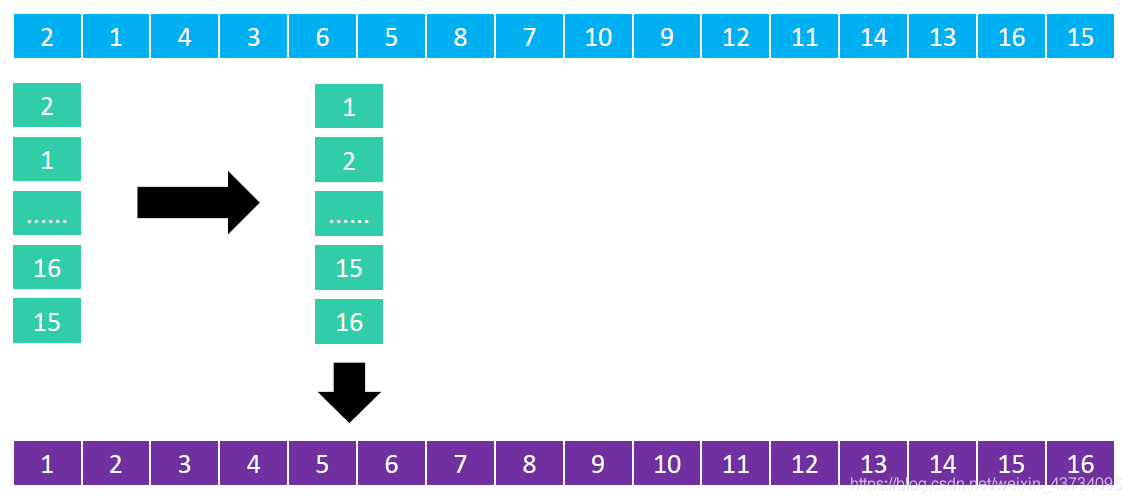
Figure 11: 最后分为 1 列

2.7.1.2 与插入排序的关系

从上面的例子中可以看出，从 8 列变为 1 列的过程中， 逆序对的数量在逐渐减少 。

而插入排序有这样一个性质： 插入排序的时间复杂度与逆序对的数量成正比关系 ，逆序对的数量越多，插入排序的时间复杂度越高。

希尔排序底层一般 使用插入排序对每一列进行排序 ，可以将希尔排序看作是对插入排序的改进。

2.7.2 代码实现

protected void sort() {
    List<Integer> steps = shellStepSequence();
    for (Integer step : steps) {
        doSort(step);
    }
}

// 留意数组下标的转换
private void doSort(int step) {
    // 基本插入排序实现（交换法）
    for (int col = 0; col < step; col++) {
        for (int i = col + step; i < array.length; i += step) {
            for (int j = i; j > col; j -= step) {
                if (compare(j - step).gt(j)) {
                    swap(j - step, j);
                } else {
                    break;
                }
            }
        }
    }
}

/**
 * 希尔算法默认使用的步长序列
 */
public List<Integer> shellStepSequence(){
    // return Arrays.asList(500, 250, 100, 50, 10, 1);
    List<Integer> stepSequence = new ArrayList<>();
    int step = 1;
    while (step < array.length) {
        stepSequence.add(0, step);
        step = step << 1;
    }
    return stepSequence;
}

3 基于空间换时间的排序算法

3.1 计数排序

适合对 一定范围内 的整数进行排序。

3.1.1 排序思路

统计每个整数在序列中出现的次数，进而推导出每个整数在有序序列中的索引。

首先找出要排序数组的中的最大值 max
根据最大值 max 开辟 max + 1 空间的数组 counts
counts 数组统计每个整数出现的次数
根据整数出现的次数，对整数进行排序
- 遍历 counts 数组，索引index即为元素值，counts[index] 为元素的出现次数
- 将 counts[index] 个 index 依次放入数组，即为排序过的序列

3.1.2 代码实现(不支持负整数)

protected void sort() {
    Integer max = Stream.of(array).max(java.util.Comparator.naturalOrder()).orElse(Integer.MIN_VALUE);
    int[] counts = new int[max + 1];
    for (Integer i : array) {
        counts[i]++;
    }
    int arrayIndex = 0;
    for (int i = 0; i < counts.length; i++) {
        int count = counts[i];
        if (count == 0) continue;
        for (int j = 0; j < count; j++) {
            array[arrayIndex++] = i;
        }
    }
}

3.1.3 优化方案

利用一个 offset 变量，即可支持负整数，且优化了空间。

protected void sort() {
    int min = Integer.MAX_VALUE;
    int max = Integer.MIN_VALUE;
    for (Integer value : array) {
        min = Math.min(min, value);
        max = Math.max(max, value);
    }
    int offset = min < 0 ? -min : 0;
    int length = (max - min + 2);
    int[] counts = new int[length];
    for (Integer i : array) {
        counts[i + offset]++;
    }
    int arrayIndex = 0;
    for (int i = 0; i < counts.length; i++) {
        int count = counts[i];
        if (count == 0) continue;
        for (int j = 0; j < count; j++) {
            array[arrayIndex++] = i - offset;
        }
    }
}

3.1.4 优化方案(稳定排序)

利用一个累计计数数组，该数组的值即为值(索引)应该放置的位置。

protected void sort() {
    int min = Integer.MAX_VALUE;
    int max = Integer.MIN_VALUE;
    for (Integer value : array) {
        min = Math.min(min, value);
        max = Math.max(max, value);
    }
    int offset = min < 0 ? -min : 0;
    int length = (max - min + 2);
    int[] counts = new int[length];
    for (Integer i : array) {
        counts[i + offset]++;
    }
    int[] aggCounts = new int[counts.length];
    int total = 0;
    for (int i = 0; i < counts.length; i++) {
        int count = counts[i];
        total += count;
        aggCounts[i] = total;
    }
    Integer[] newArray = new Integer[array.length];
    for (Integer i : array) {
        newArray[(aggCounts[i + offset] - (counts[i + offset]--))] = i;
    }
    for (int i = 0; i < array.length; i++) {
        array[i] = newArray[i];
    }
}

3.2 基数排序

基数排序通常用于整数排序（尤其是非负整数），排序思路是依次对个位数、十位数、百位数…进行排序（从低位到高位）。

private int offset;

private int radix(int value, int bit) {
    int r = 1;
    bit--;
    while (bit-- > 0) {
        r *= 10;
    }
    return (value / r) % 10 ;
}


private void countingSort(int bit) {
    int length = 10;
    int[] counts = new int[length];
    for (Integer i : array) {
        counts[radix(i + offset, bit)]++;
    }
    int[] aggCounts = new int[counts.length];
    int total = 0;
    for (int i = 0; i < counts.length; i++) {
        int count = counts[i];
        total += count;
        aggCounts[i] = total;
    }
    Integer[] newArray = new Integer[array.length];
    for (Integer i : array) {
        int radix = radix(i + offset, bit);
        newArray[(aggCounts[radix] - (counts[radix]--))] = i;
    }
    for (int i = 0; i < array.length; i++) {
        array[i] = newArray[i];
    }
}

@Override
protected void sort() {
    int min = Integer.MAX_VALUE;
    int max = Integer.MIN_VALUE;
    for (Integer value : array) {
        min = Math.min(min, value);
        max = Math.max(max, value);
    }
    offset = min < 0 ? -min : 0;
    int bits = String.valueOf(max + offset).length();
    for (int bit = 1; bit <= bits; bit++)
        countingSort(bit);

}

3.3 桶排序

排序思路：

创建一定数量的桶（比如用数组、链表作为桶）
按照一定的规则（不同类型的数据，规则不同），将序列中的元素均匀分配到对应的桶
分别对每个桶进行单独排序
将所有非空桶的元素合并成有序序列

4 性能对比

【CountingSortV3】
 稳定：✓        耗时：0.002s(2ms)        比较：0        交换：0
------------------------------------------------------------------
【CountingSortV2】
 稳定：✗        耗时：0.003s(3ms)        比较：0        交换：0
------------------------------------------------------------------
【MergeSort】
 稳定：✓        耗时：0.006s(6ms)        比较：12.05万        交换：0
------------------------------------------------------------------
【QuickSortV2】
 稳定：✗        耗时：0.006s(6ms)        比较：16.73万        交换：6821
------------------------------------------------------------------
【RadixSort】
 稳定：✓        耗时：0.007s(7ms)        比较：0        交换：0
------------------------------------------------------------------
【QuickSort】
 稳定：✗        耗时：0.007s(7ms)        比较：15.60万        交换：0
------------------------------------------------------------------
【HeapSort】
 稳定：✗        耗时：0.009s(9ms)        比较：23.69万        交换：12.42万
------------------------------------------------------------------
【ShellSortV2】
 稳定：✗        耗时：0.011s(11ms)        比较：19.56万        交换：10.73万
------------------------------------------------------------------
【ShellSort】
 稳定：✗        耗时：0.02s(20ms)        比较：64.63万        交换：52.72万
------------------------------------------------------------------
【InsertionSortV3】
 稳定：✓        耗时：0.074s(74ms)        比较：11.90万        交换：0
------------------------------------------------------------------
【InsertionSortV2】
 稳定：✓        耗时：0.143s(143ms)        比较：2510.51万        交换：0
------------------------------------------------------------------
【SelectionSort】
 稳定：✓        耗时：0.147s(147ms)        比较：5000.50万        交换：9999
------------------------------------------------------------------
【InsertionSort】
 稳定：✓        耗时：0.204s(204ms)        比较：2510.51万        交换：2509.51万
------------------------------------------------------------------
【BubbleSort】
 稳定：✓        耗时：0.626s(626ms)        比较：4999.50万        交换：2509.51万
------------------------------------------------------------------
【BubbleSortV3】
 稳定：✓        耗时：0.642s(642ms)        比较：4995.97万        交换：2509.51万
------------------------------------------------------------------
【BubbleSortV2】
 稳定：✓        耗时：0.702s(702ms)        比较：4999.01万        交换：2509.51万
------------------------------------------------------------------

Footnotes:

希尔排序

排序算法 {Back to Index} Expand All Details on Page

Table of Contents