常见算法策略
{Back to Index}
Table of Contents
1 递归
1.1 非递归转换
自行维护栈,用以 保存参数和局部变量 ,该方法本质上只是为了防止栈溢出,空间复杂度并没有优化。
1.1.1 递归写法
public static long fib(int n) { System.out.println("calculating " + n); if (n <= 2) return n; return fib(n - 2) + fib(n - 1); }
1.1.2 非递归写法
public static long fibNonRecursive(int N) { Stack<Frame> stack = new Stack(); stack.push(new Frame(N)); Map<Integer, Long> cache = new HashMap<>(); cache.put(1, (long) 1); cache.put(2, (long) 2); while (!stack.isEmpty()) { Frame frame = stack.pop(); int n = frame.n; Long r1 = cache.get(n - 1); Long r2 = cache.get(n - 2); if (r1 != null && r2 != null) { cache.put(n, r1 + r2); } else { stack.push(frame); if (r1 == null) { stack.push(new Frame(n - 1)); } if (r2 == null) { stack.push(new Frame(n - 2)); } } } return cache.get(N - 1) + cache.get(N - 2); }
2 回溯
回溯的思想是,当发现条件无法成立时,返回之前的状态,并重新进行选择。回溯适合使用递归来实现。
2.1 八皇后
2.2 迷宫
3 分治
3.1 时间复杂度定理
假设问题规模为 \(n\) ,且可以分解成 \(a\) 个规模为 \(\frac{n}{b}\) 的子问题,并在 \(O(n^d)\) 时间内将子问题合并, 这样算法复杂度的递推公式可以表示成:
\[ T(n) = aT(\frac{n}{b}) + O(n^d), a\gt0, b\gt1, d\ge0 \]
最终复杂度为:
\[ T(n) = \begin{cases} O(n^d) & d > log_ba \\ O(n^dlogn) & d = log_ba \\ O(n^{log_ba}) & d < log_ba \end{cases} \]
3.2 最大连续子序列
4 动态规划
当问题的定义是求 最值问题 ,且问题 可以采用递归的方式 , 并且递归的过程中有大量 重复子问题 的时候,则可以用动态规划求解。
4.1 使用前提
以下两个条件是是否能使用动态规划算法来解决问题的先决条件。
- 问题满足最优子结构原理
即通过求解子问题的最优解,从而可以获得原问题的最优解。 - 无后效性
指的是一旦某个状态确定,不会受历史决策影响。即只关心状态的(最优)值,而不关心是通过何种方式到达状态的。
4.2 动态规划问题特点
- 计数类
- 迷宫多少种走法
- 多少种方法选出 \(k\) 个数使得总和为 \(sum\)
- 最值类
- 最大路径权值
- 最长上升子序列长度
- 存在类
- 先手是否必胜问题
- 能否选出 \(k\) 个数使得总和为 \(sum\)
4.3 基本思路
- 先使用递归来解
- 分析在递归的过程中是否存在大量的重复子问题
- 采用备忘录(记忆化)的方式(自顶向下)来存子问题的解以避免大量的重复计算(剪枝)
- 改用 自底向上 的方式来递推,即动态规划
4.4 常规步骤
- 定义状态 \(dp(i)\)
所谓 状态 指的就是原问题,子问题的解。 - 设置初始状态
如 \(dp(0)\) 。 - 确定状态转移方程
如定义 \(dp(i)\) 和 \(dp(i-1)\) 之间的关系。
4.5 常见问题思路
4.5.1 零钱问题
假设有 25分,20分,5分,2分的硬币,现需要41分的零钱,如何使得硬币个数最少?
4.5.1.1 递归
public int coinsCountRecursion(int amount) { if (amount < 0) { return -1; } for (int coin : coins) { if (coin == amount) return 1; } int result = Integer.MAX_VALUE; for (int coin : coins) { int c = coinsCountRecursion(amount - coin); if (c == -1) continue; result = Math.min(result, c); } if (result == Integer.MAX_VALUE) return -1; return result + 1; }
4.5.1.2 记忆化
public int coinsCountRecursionWithMemorization(int amount, Map<Integer, Integer> cache) { if (amount < 0) { return -1; } if (cache.get(amount) != null) { return cache.get(amount); } for (int coin : coins) { if (coin == amount) return 1; } int result = Integer.MAX_VALUE; for (int coin : coins) { int c = coinsCountRecursionWithMemorization(amount - coin, cache); if (c == -1) continue; result = Math.min(result, c); } if (result == Integer.MAX_VALUE) return -1; cache.put(amount, result + 1); return result + 1; }
4.5.1.3 动态规划
假设 \(dp(i)\) 表示凑到 \(i\) 分所需的最少硬币个数,则:
\[ dp(i) = min\{dp(i-25),dp(i-20),dp(i-5),dp(i-2)\} + 1 \]
初始状态为: \(dp[i] = 1 , i \in [25, 20, 5, 2]\) 。
public int coinsCountDP(int amount) { int[] dp = new int[amount + 1]; dp[0] = 0; List<Integer> allCoins = new ArrayList<>(); for (int coin : coins) { allCoins.add(coin); } Map<Integer, Integer> chosenCoins = new HashMap<>(); // amount -> chosenCoin for (int i = 1; i < dp.length; i++) { if (allCoins.contains(i)) { dp[i] = 1; chosenCoins.put(i, i); continue; } int m = Integer.MAX_VALUE; int chosenCoin = coins[0]; for (int coin : coins) { if (i - coin < 0) continue; if (dp[i - coin] == -1) continue; if (dp[i - coin] < m) { m = dp[i - coin]; chosenCoin = coin; } } if (m == Integer.MAX_VALUE) { dp[i] = -1; } else { dp[i] = m + 1; chosenCoins.put(i, chosenCoin); } } if (dp[amount] != -1) { System.out.print("[" + amount + "] = "); int start = amount; while (start != 0) { System.out.print(chosenCoins.get(start) + " "); start -= chosenCoins.get(start); } System.out.println(); } return dp[amount]; }
4.5.2 最大连续子序列和问题
例如 -2, 1, -3, 4, -1, 2, 1, -5, 4 ,则最大连续子序列和为 4 + (-1) + 2 + 1 = 6
4.5.2.1 递归
public int maximumSubArrayRecursive() { int max = Integer.MIN_VALUE; for (int i = 0; i < numbers.length; i++) { max = Math.max(max, maximumSubArrayRecursive(i)); } return max; } // 该函数的返回值表示:以第 n 个元素作为结尾的最大连续子序列和 private int maximumSubArrayRecursive(int n) { // n = [0, numbers.len) if (n == 0) return numbers[0]; if (maximumSubArrayRecursive(n - 1) <= 0) { return numbers[n]; } else { return maximumSubArrayRecursive(n - 1) + numbers[n]; } }
4.5.2.2 动态规划
假设 \(numbers\) 为整个序列,使用 \(dp(i)\) 表示以 \(numbers[i]\) 结尾的最大连续子序列和,则:
\[ dp(i) = \begin{cases} numbers[i] & dp(i-1) \le 0 \\ dp(i-1) + numbers[i] & dp(i-1) > 0 \end{cases} \]
初始状态为 \(dp(0) = numbers[0]\) 。
public int maximumSubArrayDP() { int[] dp = new int[numbers.length]; dp[0] = numbers[0]; for (int i = 1; i < numbers.length; i++) { if (dp[i - 1] <= 0) { dp[i] = numbers[i]; } else { dp[i] = dp[i - 1] + numbers[i]; } } return Ints.max(dp); }
4.5.3 最长递增子序列(LIS)长度问题
例如 [10, 2, 2, 5, 1, 7, 101, 18] ,其最长递增子序列为 [2, 5, 7, 101] 或 [2, 5, 7, 18] 。
4.5.3.1 递归
public int lis() { int[] result = new int[numbers.length]; for (int i = 0; i < numbers.length; i++) { result[i] = lisRecursive(i); } return Ints.max(result); } // 返回值表示:以第 n 个元素作为结尾的最长上升子序列的个数 public int lisRecursive(int n) { if (n == 0) return 1; List<Integer> candidates = new ArrayList<>(); for (int i = n - 1; i >= 0; i--) { if (numbers[i] < numbers[n]) { candidates.add(lisRecursive(i)); } } if (candidates.isEmpty()) return 1; return candidates.stream().max(Comparator.naturalOrder()).get() + 1; }
4.5.3.2 动态规划 [\(O(n^2)\)]
假设 \(dp(i)\) 是以 \(numbers[i]\) 结尾的最长递增子序列的长度,则:
\[ dp(i) = max\{dp(j)\}, j \in [0, i) \]
最长递增子序列的长度为:
\[ max\{dp(i)\}, i\in[0, numbers.length) \]
public int lisDP() { int[] dp = new int[numbers.length]; dp[0] = 1; for (int i = 1; i < numbers.length; i++) { int[] candidates = new int[i]; for (int j = i - 1; j >=0; j--) { if (numbers[j] < numbers[i]) { candidates[j] = dp[j]; } } dp[i] = Ints.max(candidates) + 1; } return Ints.max(dp); }
4.5.3.3 其他思路 [\(O(nlogn)\)]
- 将每个数字看作扑克牌,遍历每一个数字
- 将每个扑克牌压在第一个牌顶数字大于等于它自身的牌堆上面
- 如找不到满足要求的牌堆,则新建一个牌堆
- 最终的牌堆数量就是最长递增子序列的长度
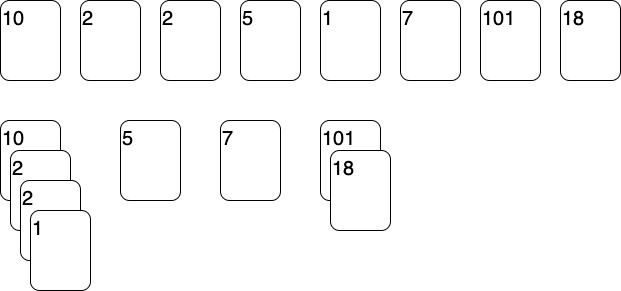
Figure 1: 思路示意
4.5.4 最长公共子序列(LCSubsequence)长度问题
如 [1, 3, 5, 9, 10] 和 [1, 4, 9, 10] 的最长公共子序列长度为 3 ([1, 9, 10])
4.5.4.1 递归
public int lcs() { return lcsRecursive(seq1.length - 1, seq2.length - 1); } public int lcsRecursive(int i, int j) { if (i == 0 && j == 0) { if (seq1[0] != seq2[0]) return 0; return 1; } if (i == 0) { for (int k = 0; k < j; k++) { if (seq1[0] == seq2[k]) return 1; } return 0; } if (j == 0) { for (int k = 0; k < i; k++) { if (seq1[k] == seq2[0]) return 1; } return 0; } if (seq1[i] == seq2[j]) { return 1 + lcsRecursive(i - 1, j - 1); } else { return Ints.max( lcsRecursive(i - 1, j), // [1, 2, 3, 4] vs [1, 2, 3] lcsRecursive(i, j - 1) // [1, 2, 3] vs [1, 2, 3, 4] ); } }
4.5.4.2 动态规划
假设 \(dp(i, j)\) 是 \(seq1\) 前 \(i\) 个元素与 \(seq2\) 前 \(j\) 个元素的最长公共子序列长度,则:
\[ dp(i,j) = \begin{cases} 1 + dp(i-1, j-1) & seq1[i] == seq2[j] \\ max\{dp(i-1, j), dp(i, j-1)\} \end{cases} \]
最长公共子序列长度为:
\[ dp[seq1.length - 1][seq2.length - 1] \]
public int lcsDP() { int[][] dp = new int[seq1.length][seq2.length]; if (seq1[0] != seq2[0]) { dp[0][0] = 0; } else { dp[0][0] = 1; } for (int i = 0; i < seq1.length; i++) { for (int j = 0; j < seq2.length; j++) { if (i == 0 && j == 0) continue; if (i == 0) { boolean flag = false; for (int k = 0; k < j; k++) { if (seq1[0] == seq2[k]) { flag = true; break; } } if (flag) { dp[i][j] = 1; } else { dp[i][j] = 0; } continue; } if (j == 0) { boolean flag = false; for (int k = 0; k < i; k++) { if (seq1[k] == seq2[0]) { flag = true; break; } } if (flag) { dp[i][j] = 1; } else { dp[i][j] = 0; } continue; } if (seq1[i] == seq2[j]) { dp[i][j] = 1 + dp[i-1][j-1]; } else { dp[i][j] = Ints.max( // dp[i-1][j-1], dp[i-1][j], dp[i][j-1] ); } } } return dp[seq1.length - 1][seq2.length - 1]; }
优化如下:
public int lcsDP2() { int[][] dp = new int[seq1.length][seq2.length]; if (seq1[0] != seq2[0]) { dp[0][0] = 0; } else { dp[0][0] = 1; } for (int i = 0; i < seq1.length; i++) { for (int j = 0; j < seq2.length; j++) { if (i == 0 && j == 0) continue; if (seq1[i] == seq2[j]) { dp[i][j] = 1 + v(dp, i-1, j-1); } else { dp[i][j] = Ints.max( v(dp, i-1, j), v(dp, i, j-1) ); } } } return dp[seq1.length - 1][seq2.length - 1]; } private int v(int[][] dp, int i, int j) { if (i < 0) return Integer.MIN_VALUE; if (j < 0) return Integer.MIN_VALUE; return dp[i][j]; }
4.5.5 最长公共子串(LCString)长度问题
如 [1, 3, 4, 5, 7] 和 [2, 4, 5, 7, 8] ,最长公共子串长度为 3 ([4, 5, 7])
4.5.5.1 递归
public int lcs() { int max = Integer.MIN_VALUE; for (int i = 0; i < seq1.length; i++) { for (int j = 0; j < seq2.length; j++) { max = Ints.max(lcs(i, j), max); } } return max; } public int lcs(int i, int j) { // if (i < 0 || j < 0) return Integer.MIN_VALUE; if (i == 0 && j == 0) { if (seq1[0] == seq2[0]) return 1; return 0; } if (i == 0) { if (seq1[0] == seq2[j]) return 1; return 0; } if (j == 0) { if (seq1[i] == seq2[0]) return 1; return 0; } if (seq1[i] == seq2[j]) { return 1 + lcs(i - 1, j - 1); } else { return 0; } }
4.5.5.2 动态规划
假设 \(dp(i, j)\) 是以 \(seq1[i]\) 与 \(seq2[j]\) 结尾 的最长公共子串长度,则:
\[ dp(i,j) = \begin{cases} 0, & i == j == 0, seq1[0] \ne seq2[0] \\ 1, & i == j == 0, seq1[0] == seq2[0] \\ 1 + dp(i-1, j-1), & seq1[i] == seq2[j] \\ 0, & seq1[i] \ne seq2[j] \end{cases} \]
最长公共子串长度为:
\[ max\{dp[i][j]\}, i \in [0, seq1.length), j \in [0, seq2.length) \]
public int lcsDP() { int[][] dp = new int[seq1.length][seq2.length]; if (seq1[0] == seq2[0]) { dp[0][0] = 1; } else { dp[0][0] = 0; } int max = Integer.MIN_VALUE; for (int i = 0; i < seq1.length; i++) { for (int j = 0; j < seq2.length; j++) { if (i == 0) { if (seq1[0] == seq2[j]) { dp[i][j] = 1; max = Ints.max(max, 1); } continue; } if (j == 0) { if (seq1[i] == seq2[0]) { dp[i][j] = 1; max = Ints.max(max, 1); } continue; } if (seq1[i] == seq2[j]) { dp[i][j] = 1 + dp[i-1][j-1]; max = Ints.max(max, dp[i][j]); } } } return max; }
4.5.6 0/1 背包问题
有 \(n\) 件物品和最大承重为 \(W\) 的背包,每件物品重量为 \(w_i\) 价值为 \(v_i\) ,
如何在保证总重量不超 \(W\) 的前提下背包总价值最大。
0/1 指的是每件物品最多只能选择1件。
4.5.6.1 递归
public long maxValue() { return maxValue(items, total); } public long maxValue(List<Item> items, long total) { if (total <= 0) return 0; if (items.isEmpty()) return 0; long[] candidates = new long[items.size()]; for (int i = 0; i < items.size(); i++) { Item item = items.get(i); candidates[i] = item.value + maxValue(newItems(items, i), total - item.value); } return Longs.max(candidates); } private List<Item> newItems(List<Item> originItems, int indexOfItemToBeRemoved) { assert indexOfItemToBeRemoved < originItems.size(); List<Item> result = new ArrayList<>(); for (int i = 0; i < originItems.size(); i++) { if (i != indexOfItemToBeRemoved) result.add(originItems.get(i)); } return result; }
4.5.6.2 动态规划
假设 \(dp(i, j)\) 代表最大承重为 \(j\) ,当有前 \(i\) 件物品可选时的最大总价值,则:
\[ d(i, j) = max\{dp(i-1, j), v_i + dp(i-1, j-w_i)\}\]
最终问题的解为: \(dp(n, W)\)
public int maxValueDP() { return maxValueDP(items.size(), total); } public int maxValueDP(int n, int total) { int[][] dp = new int[n + 1][total + 1]; for (int t = 0; t <= total; t++) { for (int i = 1; i <= n; i++) { if (t == 0) { dp[i][t] = 0; continue; } Item item = items.get(i - 1); if (t - item.weight >= 0 && (i - 1) >= 0) { dp[i][t] = Ints.max( item.value + dp[i-1][t - item.weight], // choose last item dp[i - 1][t] // don't choose last item ); } } } return dp[n][total]; }
4.5.6.3 恰好装满
即需要满足总重量 正好 为 \(W\) 这个条件。
4.5.6.3.1 递归
public int maxValueExactly() { return maxValueExactly(items, total); } public int maxValueExactly(List<Item> items, long total) { if (total == 0) return 0; if (total < 0) return -1; if (items.isEmpty()) { return -1; } int[] candidates = new int[items.size()]; for (int i = 0; i < items.size(); i++) { Item item = items.get(i); int c = maxValueExactly(newItems(items, i), total - item.weight); if (c == -1) { candidates[i] = -1; } else { candidates[i] = item.value + c; } } int max = Ints.max(candidates); return max == -1 ? -1 : max; }
4.5.6.3.2 动态规划
public int maxValueDPExactly() { return maxValueDPExactly(items.size(), total); } public int maxValueDPExactly(int n, int total) { int[][] dp = new int[n + 1][total + 1]; for (int t = 0; t <= total; t++) { for (int i = 1; i <= n; i++) { if (t == 0) { dp[i][t] = 0; continue; } Item item = items.get(i - 1); if (i == 1) { dp[i][t] = (item.weight == t) ? item.value : -1; continue; } if (t - item.weight >= 0 && (i - 1) >= 0) { dp[i][t] = Ints.max( dp[i-1][t - item.weight] == -1 ? -1 : item.value + dp[i-1][t - item.weight], // choose last item dp[i - 1][t] // don't choose last item ); } } } return dp[n][total]; }