树
{Back to Index}

1. 二叉树性质
- 1.1. 完全二叉树性质
2. 二叉搜索树(BST)
3. AVL
4. B 树
5. B+ 树
- 5.1. 特点
- 5.2. 数据库为何选择 B+ 树
6. 红黑树
7. 二叉堆
8. Union Find (动态连通性)

1 二叉树性质

如果叶子节点个数为 \(n_0\) ，度为 2 的节点个数为 \(n_2\) ，则 \(n_0 = n_2 + 1\) ，推理过程如下：

假设度为 1 的节点数量为 \(n_1\) ，则二叉树总节点数为 \(n = n_0 + n_1 + n_2\) 。
考虑到二叉树的总边数 T 为 \(T = n_1 + 2 * n_2\) ，也可以看作 \(T = n - 1\) (除了根节点的每个节点和父节点之间就是一条边) 。

1.1 完全二叉树性质

参见 7.1.1

2 二叉搜索树(BST)

2.1 接口

int size();
boolean isEmpty();
void clear();
void add(E element);
void remove(E element);
boolean contains(E element);

2.2 添加节点

找到应该插入位置的 parent
创建新节点 node
\(parent.left = node\) 或者 \(parent.right = node\)

public void add(@NonNull E element) {
    if (root == null) { // first node
        root = new Node<>(element, null);
        size++;
        return;
    }

    Node<E> node = root;
    Node<E> parent = root;
    int position = LEFT;
    while (node != null) {
        parent = node;
        int cmp = element.compareTo(node.element);
        if (cmp > 0) {
            node = node.right;
            position = RIGHT;
        } else if (cmp < 0) {
            node = node.left;
            position = LEFT;
        } else {
            node.element = element;
            return;
        }
    }
    Node<E> newNode = Node.of(element, parent);
    if ( position == LEFT ) {
        parent.left = newNode;
    } else {
        parent.right = newNode;
    }
}

2.3 删除节点

可以分三种情况分析：(但最终只会删除度为 0 或 1 的节点)

删除 度=0 的节点（叶子节点）

直接将父节点中子节点指针设为 null 即可。
删除 度=1 的节点

用被删节点的子节点替代被删节点即可。
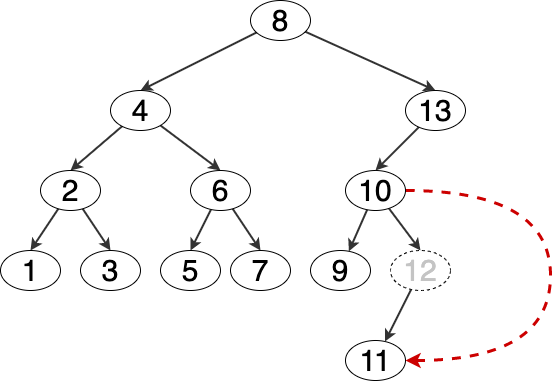
删除 度=2 的节点

被删除节点的值(element)设置为前驱节点或后继节点的值，并删除前驱或后继节点。
这里用到了一个性质： 如果一个节点的度为 2 ，则该节点的前驱或后继节点的度只能是 0 或 1 。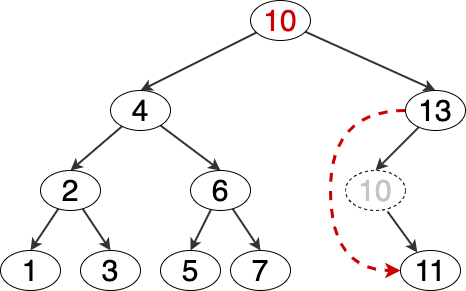

public void remove(Node<E> node) {
    if (node == null) return;
    if (node.degree() == 0) {
        if (node.parent == null) {
            root = null;
            size--;
            return;
        }
        if (node.isLeft()) {
            node.parent.left = null;
            size--;
        } else {
            node.parent.right = null;
            size--;
        }
    } else if (node.degree() == 1) {
        Node<E> child = node.left != null ? node.left : node.right;
        if (node.parent == null) {
            child.parent = null;
            root = child;
            size--;
            return;
        }
        child.parent = node.parent;
        if (node.isLeft()) {
            node.parent.left = child;
            size--;
        } else {
            node.parent.right = child;
            size--;
        }
    } else { // degree == 2
        Node<E> predecessor = node.predecessor();
        if (predecessor != null) {
            node.element = predecessor.element;
            remove(predecessor);
        } else {
            Node<E> successor = node.successor();
            node.element = successor.element;
            remove(successor);
        }
    }
}

2.4 非递归遍历

2.4.1 前序遍历

public void preOrderTraverse(Consumer<E> visitor) {
    preOrderTraverse(root, visitor);
}

private void preOrderTraverse(Node<E> root, Consumer<E> visitor) {
    if (root == null) return;
    Stack<Node<E>> stack = new Stack<>();
    stack.push(root);
    while (!stack.isEmpty()) {
        Node<E> node = stack.pop();
        visitor.accept(node.element);
        if (node.right != null) stack.push(node.right);
        if (node.left != null) stack.push(node.left);
    }
}

2.4.2 中序遍历

public void inOrderTransverse(Consumer<E> visitor) {
    inOrderTransverse(root, visitor);
}

private void inOrderTransverse(Node<E> root, Consumer<E> visitor) {
    if (root == null) return;
    Stack<Node<E>> stack = new Stack<>();
    stack.push(root);
    Node<E> prev = null; // last popped node
    while (!stack.isEmpty()) {
        Node<E> node = stack.pop();
        if (node.isLeaf() || isAncestor(node, prev)) {
            prev = node;
            visitor.accept(node.element);
        } else {
            if (node.right != null) {
                stack.push(node.right);
                prev = node.right; // notice this line !!
            }
            stack.push(node);
            if (node.left != null) {
                stack.push(node.left);
                // prev = node.left;
            }
        }
    }
}

// private void inOrderTransverse(Node<E> root, Consumer<E> visitor) {
//     if (root == null) return;
//     Stack<Node<E>> stack = new Stack<>();
//     Node<E> node = root;
//     while (!stack.isEmpty() || node != null) {
//         if (node != null) {
//             stack.push(node);
//             node = node.left;
//         } else {
//             node = stack.pop();
//             visitor.accept(node.element);
//             node = node.right;
//         }
//     }
// }

2.4.3 后序遍历

public void postOrderTransverse(@NonNull Consumer<E> visitor) {
    postOrderTransverse(root, visitor);
}

private void postOrderTransverse(Node<E> root, Consumer<E> visitor) {
    if (root == null) return;
    Stack<Node<E>> stack = new Stack<>();
    stack.push(root);
    Node<E> prev = null; // last popped node
    while (!stack.isEmpty()) {
        Node<E> top = stack.peek();
        if (top.isLeaf() || isParent(top, prev)) {
            prev = stack.pop();
            visitor.accept(prev.element);
        } else {
            if (top.right != null) stack.push(top.right);
            if (top.left != null) stack.push(top.left);
        }
    }
}

2.5 翻转

public BinaryTree<E> invert() {
    invert(root);
    return this;
}

private void invert(Node<E> node) {
    if (node == null) return;
    Node<E> tmp = node.left;
    node.left = node.right;
    node.right = tmp;
    invert(node.left);
    invert(node.right);
}

2.6 层序遍历

因为被先访问的节点，则其子节点也会被先访问到，因此可以使用队列来实现：

将根节点入队
循环执行下述操作，直到队列为空
1. 队头 H 出队（访问）
2. H 的左右节点入队

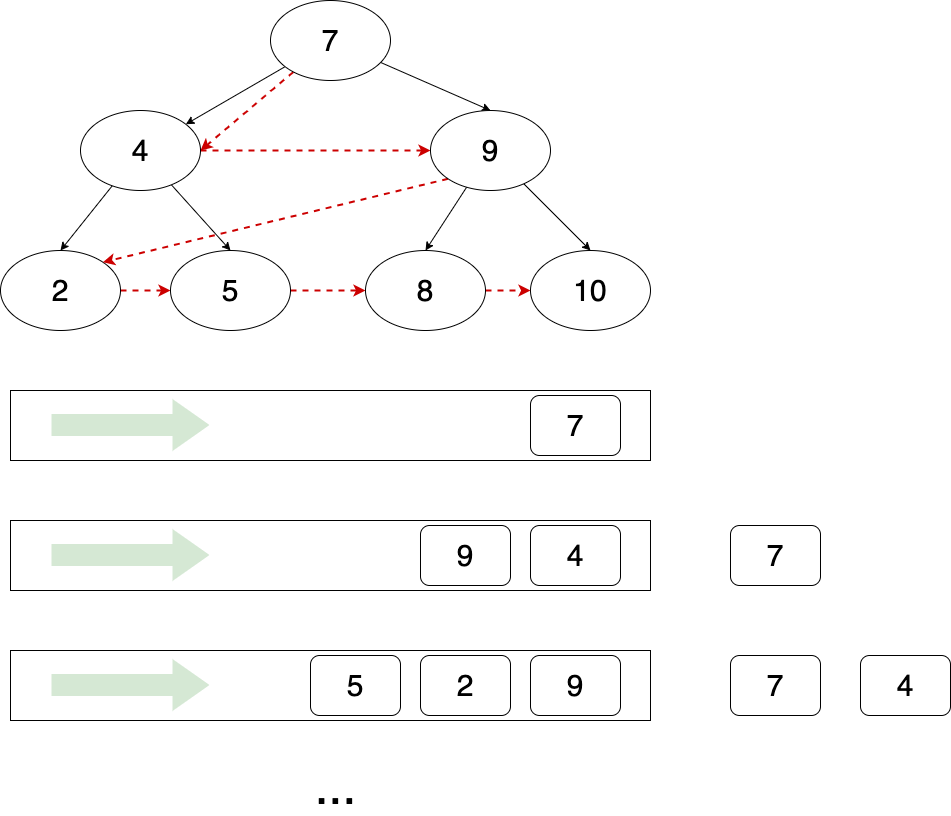
Figure 3: 遍历顺序

public void levelTraverse() {
    if ( root == null ) return;
    Queue<Node<E>> queue = new LinkedList<>();
    queue.offer(root);
    Node<E> head;
    while ( (head = queue.poll()) != null ) {
        System.out.print(head.element + " ");
        if ( head.left != null ) {
            queue.offer(head.left);
        }
        if ( head.right != null ) {
            queue.offer(head.right);
        }
    }
}

层序遍历常用于：

计算树的高度
判断是否为完全二叉树

2.6.1 计算树的高度

使用递归

public int height(Node<E> node) {
    if ( node == null ) return 0;
    return Math.max(height(node.left), height(node.right)) + 1;
}

使用层序遍历迭代

当一层遍历完毕，则层数加 1 。

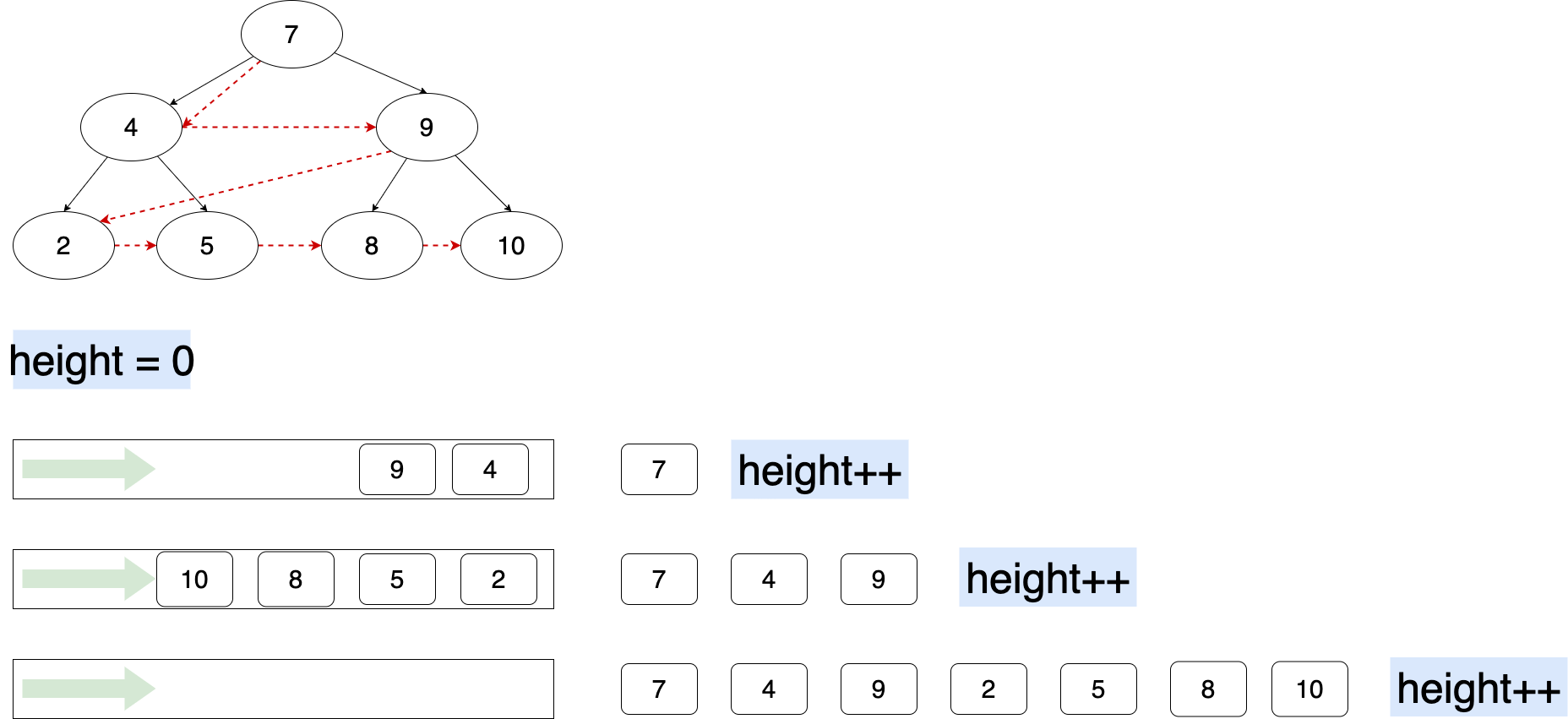
Figure 4: 使用层序遍历计算树的高度

public int height() {
    return height(root);
}
public int height(Node<E> node) {
    if ( node == null ) return 0;
    Queue<Node<E>> queue = new LinkedList<>();
    queue.offer(root);
    int numOfNodesLeftForLayer = 1;
    int height = 0;
    while ( !queue.isEmpty() ) {
        Node<E> head = queue.poll();
        numOfNodesLeftForLayer--;
        if ( head.left != null ) {
            queue.offer(head.left);
        }
        if ( head.right != null ) {
            queue.offer(head.right);
        }
        if ( numOfNodesLeftForLayer == 0 ) {
            height++;
            numOfNodesLeftForLayer = queue.size();
        }
    }
    return height;
}

2.6.2 是否为完全二叉树

完全二叉树指的是最后一层节点 左对齐 的二叉树。

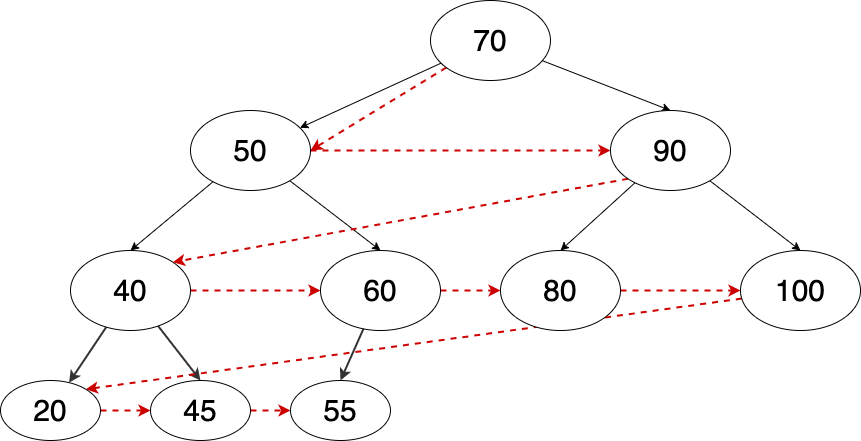
Figure 5: 完全二叉树

使用层序遍历来判断是否为完全二叉树的思路是，对需要入队的节点的度进行分类比较：

度为 2
左右子节点正常入队
度为 1
- 仅有右子节点
  不是完全二叉树
- 仅有左子节点
  后续节点必须都是叶子，才是完全二叉树
度为 0
后续节点必须都是叶子，才是完全二叉树

public boolean isComplete() {
    if ( root == null ) return false;
    Queue<Node<E>> queue = new LinkedList<>();
    queue.offer(root);
    boolean leftHasToBeLeaf = false;
    while ( !queue.isEmpty() ) {
        Node<E> head = queue.poll();
        if ( leftHasToBeLeaf && !head.isLeaf() ) return false;
        if (head.left != null && head.right != null) {
            queue.offer(head.left);
            queue.offer(head.right);
        } else if (head.right == null) {
            leftHasToBeLeaf = true;
        } else { // head.left == null && head.right != null
            return false;
        }
    }
    return true;
}

2.7 前驱/后继节点

当前节点的前驱节点，指的比当前节点小的前一个节点。

如果有左子树，则为左子树中的最大节点 (如图例的 8 ，其前驱为 7)
如果左子树为空，则为第一个比它小的父节点 (如图例中的 9 ，其前驱为 8)
这个条件可以等效于递归向上找到第一个父节点，而当前节点处于该父节点的右子树中，即第一个小于该节点的父节点。
其余情况不存在前驱节点 (如图例中的 1 和 8)

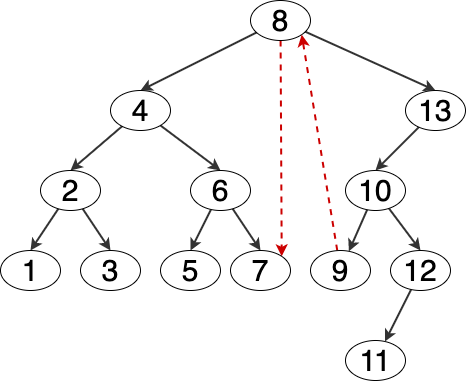
Figure 6: 前驱节点图例

public Node<E> predecessor() {
    if (left != null) {
        Node<E> node = left;
        while (left.right != null) left = left.right;
        return left;
    } else { // left == null
        // if (parent == null) return null;
        Node<E> node = parent;
        while (true) {
            if (node == null) return null;
            if (node.parent.right == node) return node.parent;
            node = node.parent;
        }
    }
}

后继节点，指的是中序遍历时，位于当前节点之后的第一个节点。

如果有右子树，则为右子树中的最小（左）节点
如果右子树为空，则为第一个比它大的父节点
其余情况不存在后继节点

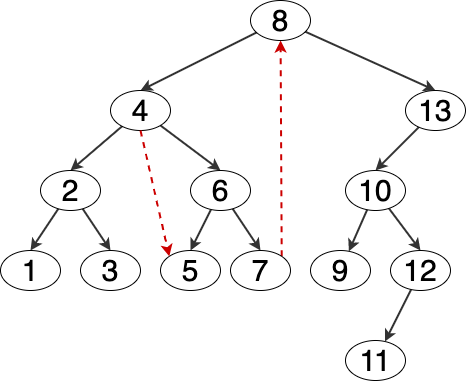
Figure 7: 后继节点图例

3 AVL

AVL 树每个节点的平衡因子的绝对值小于 1 。所谓的平衡因子就是左右子树的 高度差 。

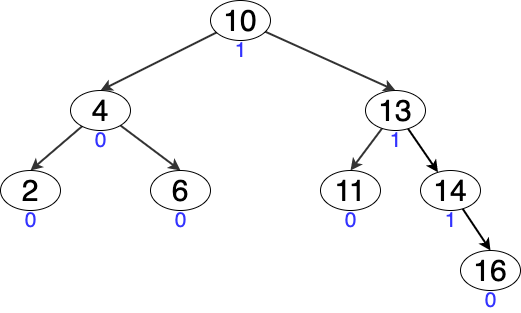
Figure 8: AVL 树

3.1 失衡

3.1.1 性质

导致 祖先节点 失衡， 最坏情况 是所有祖先节点都失衡
父节点和非祖先节点不会失衡

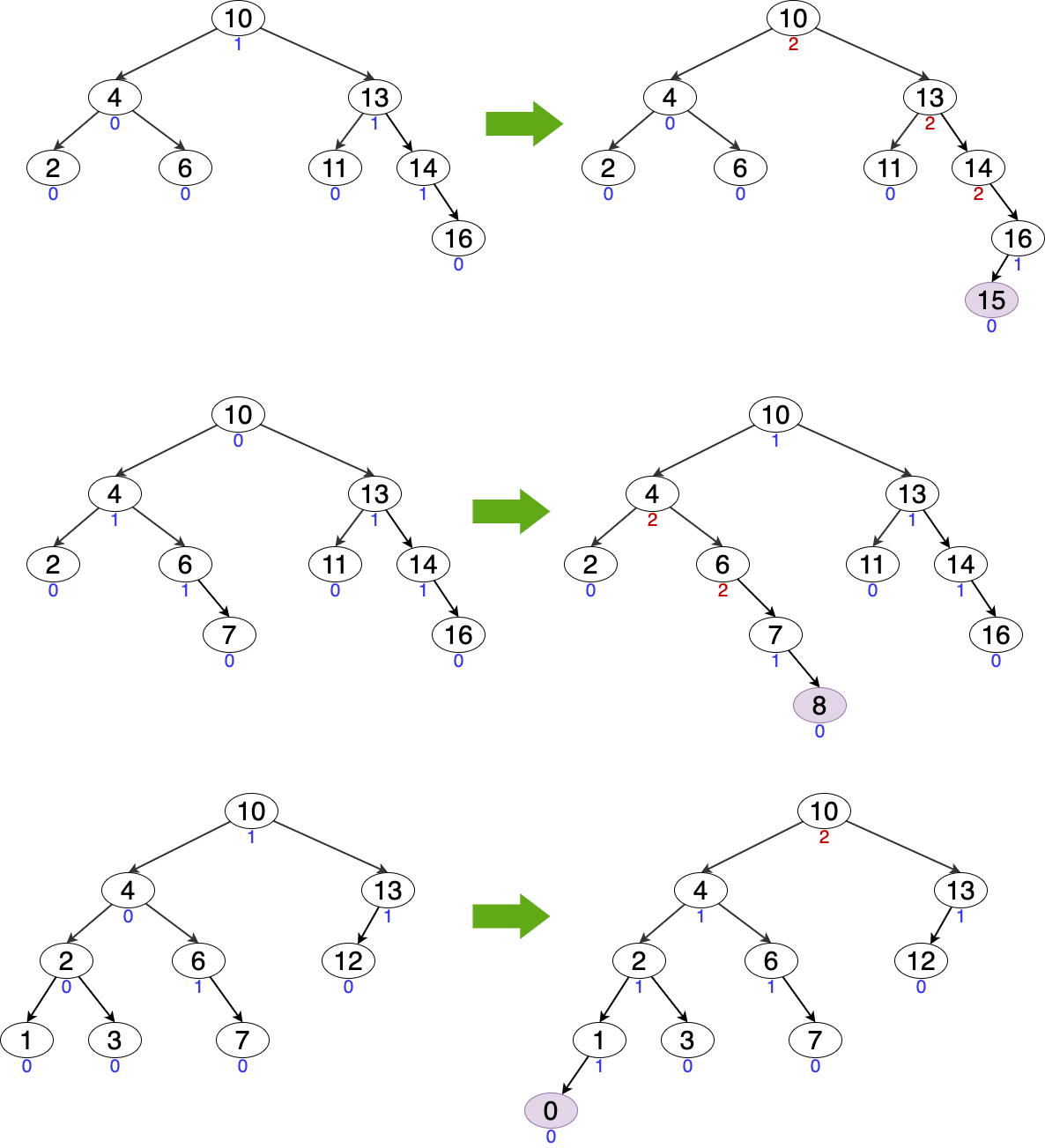
Figure 9: 失衡 AVL 树

3.2 添加节点

添加节点可能会导致所有祖先节点都失衡，但是 只要让高度最低的失衡节点恢复平衡 ，整棵树就恢复平衡了。(\(O(1)\))

3.2.1 通过旋转重平衡

LL/RR/LR/RL 是导致失衡的所有情况。

protected void nodeAdded(Node<E> node) {
    super.nodeAdded(node);
    Node<E> n = node;
    Node<E> p = node;
    Node<E> g = node.parent;
    while (g != null) {
        ((AVLNode<E>) g).updateHeight();
        if (!((AVLNode<E>) g).isBalanced()) {
            balance(g, p, n); // will update height for g and p when doing balancing
            break;
        }
        n = p;
        p = g;
        g = g.parent;
    }
}

private void balance(Node<E> g0, Node<E> p0, Node<E> n0) {
    AVLNode<E> g = (AVLNode<E>) g0;
    AVLNode<E> p = (AVLNode<E>) p0;
    AVLNode<E> n = (AVLNode<E>) n0;
    if (g.left != null && n == g.left.left) {
        rightRotate(g);
    } else if (g.right != null && n == g.right.right) {
        leftRotate(g);
    } else if (g.right != null && n == g.right.left) {
        rightRotate(p);
        leftRotate(g);
    } else if (g.left != null && n == g.left.right) {
        leftRotate(p);
        rightRotate(g);
    }
}

这里还有一种算法可以确定 g/p/n ，即 p 为 g 较高的子树，n 为 p 较高的子树。

private void balance(Node<E> g0) {
        AVLNode<E> g = (AVLNode<E>) g0;
        AVLNode<E> p = g.higher();
        AVLNode<E> n = p.higher();
        balance(g, p, n);
}

3.2.1.1 右旋转

旋转是针对祖父节点相对父节点而言的，当插入的新元素位于 g.left.left 中，且造成 g 节点失衡，则 g 节点需要右旋转。

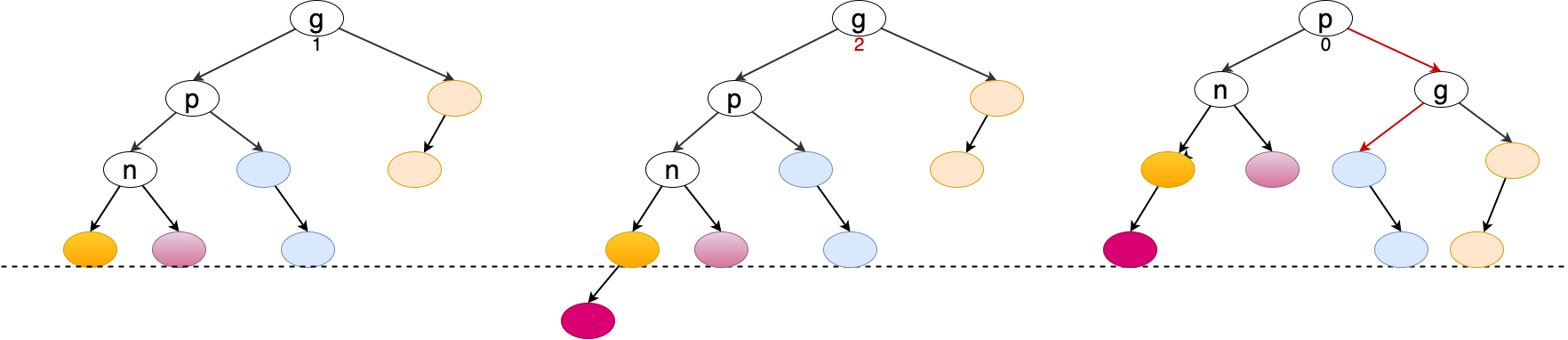
public void rightRotate(Node<E> node) {
    Node<E> p = node.left;
    Node<E> t3 = p.right;

    p.right = node;
    node.left = t3;
    if (node.isLeft()) {
        node.parent.left = p;
    } else if (node.isRight()) {
        node.parent.right = p;
    } else { // node is root
        root = p;
    }

    p.parent = node.parent;
    node.parent = p;
    if (t3 != null) t3.parent = node;

    ((AVLNode<E>) node).updateHeight();
    ((AVLNode<E>) p).updateHeight();
}

3.2.1.2 左旋转

旋转是针对祖父节点相对父节点而言的，当插入的新元素位于 g.right.right 中，且造成 g 节点失衡，则 g 节点需要左旋转。

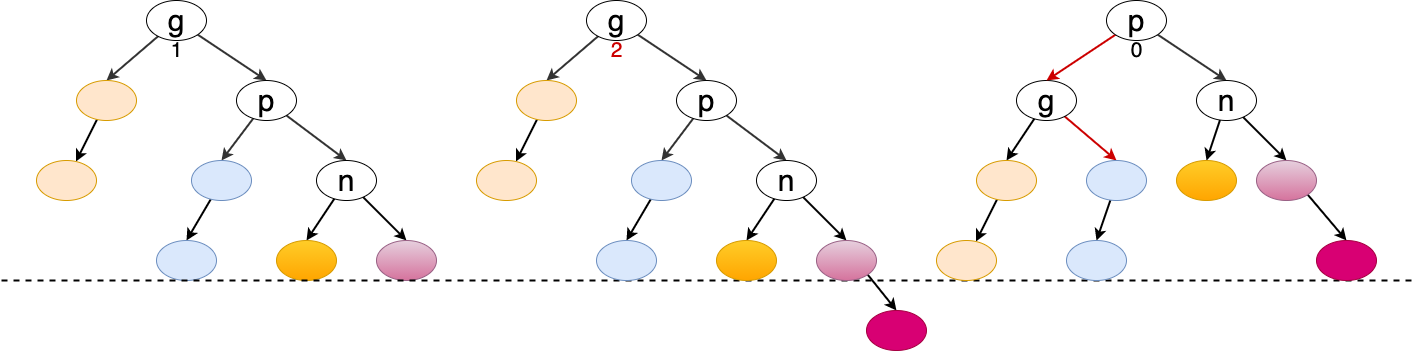
public void leftRotate(Node<E> node) {
    Node<E> p = node.right;
    Node<E> t1 = p.left;

    node.right = t1;
    p.left = node;
    if (node.isLeft()) {
        node.parent.left = p;
    } else if (node.isRight()) {
        node.parent.right = p;
    } else { // node is root
        root = p;
    }

    p.parent = node.parent;
    node.parent = p;
    if (t1 != null) t1.parent = node;

    ((AVLNode<E>) node).updateHeight();
    ((AVLNode<E>) p).updateHeight();
}

3.2.1.3 先左后右旋转

当插入的新元素位于 \(g.left.right\) 中，且造成 g 节点失衡，则 p 节点先左旋转，然后 g 节点右旋转。

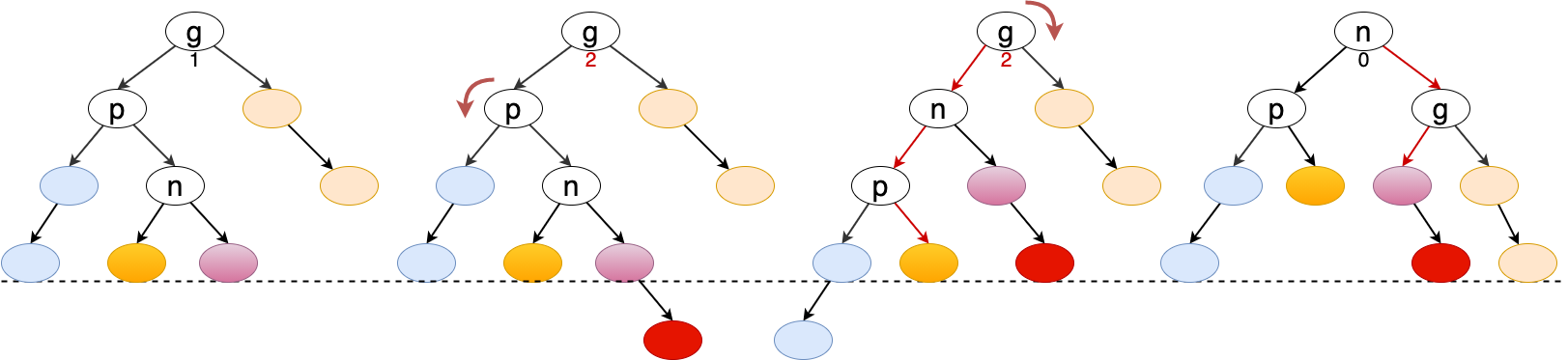
3.2.1.4 先右后左旋转

当插入的新元素位于 \(g.right.left\) 中，且造成 g 节点失衡，则 p 节点先右旋转，然后 g 节点左旋转。

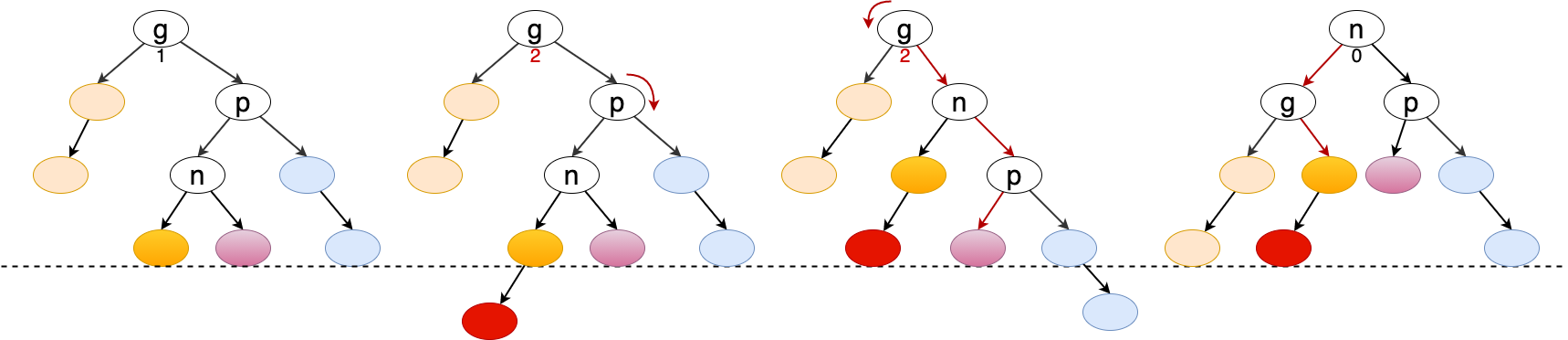
3.2.2 不通过旋转的重平衡

从下图的分析中可以看出，旋转前后，节点 a/b/c/d/e/f/g 的顺序始终保持不变。
平衡后的结果始终为 b 为 a/c 的根节点，f 为 e/g 的根节点，而 d 为 b/f 的根节点。
可以利用这一性质实现更为通用的重平衡算法。

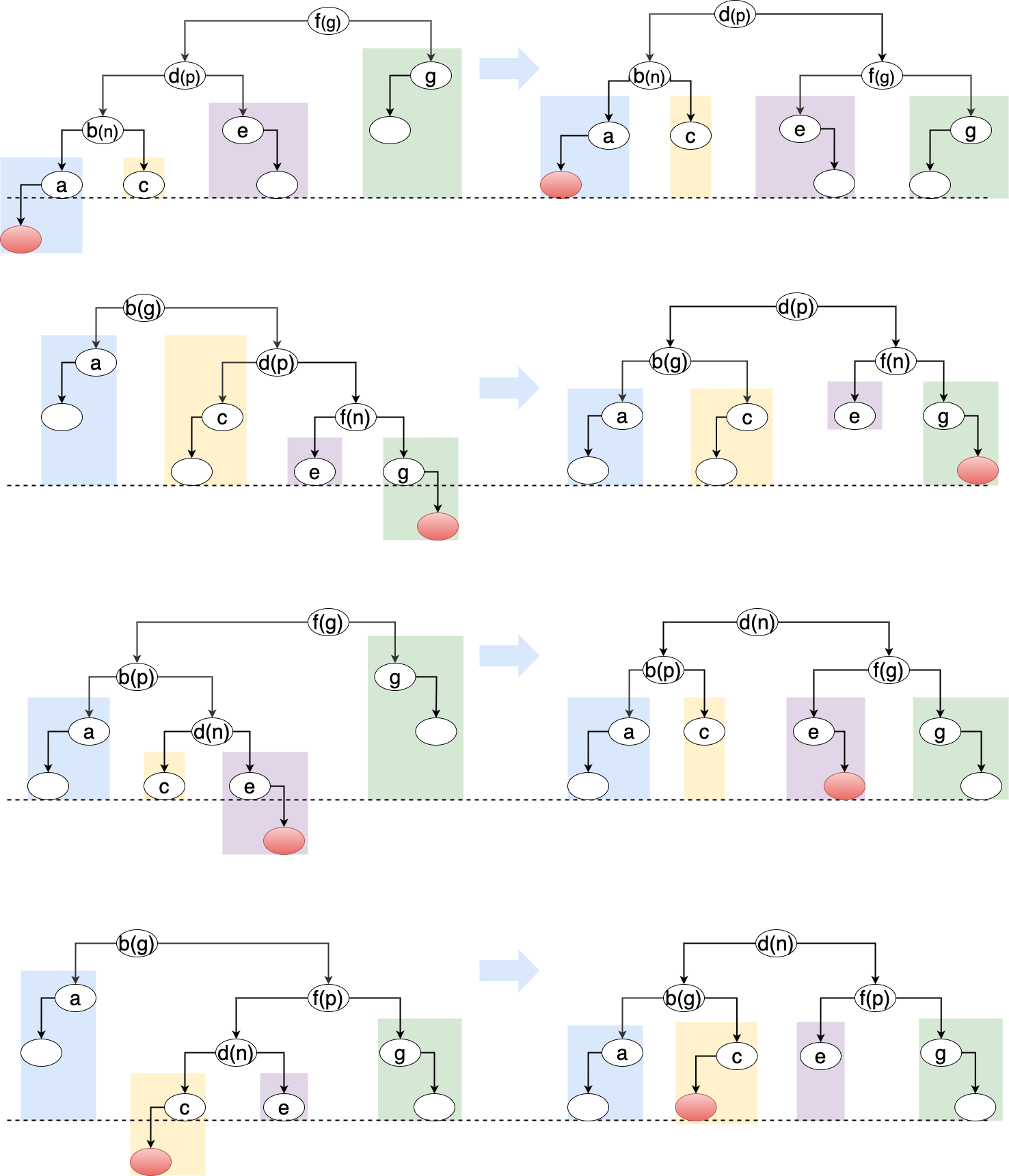
Figure 14: 更为通用的重平衡算法

private void balance(Node<E> g0, Node<E> p0, Node<E> n0) {
    AVLNode<E> g = (AVLNode<E>) g0;
    AVLNode<E> p = (AVLNode<E>) p0;
    AVLNode<E> n = (AVLNode<E>) n0;
    if (g.left != null && n == g.left.left) {
        balance(n.left, n, n.right, p, p.right, g, g.right, g);
    } else if (g.right != null && n == g.right.right) {
        balance(g.left, g, p.left, p, n.left, n, n.right, g);
    } else if (g.right != null && n == g.right.left) {
        balance(g.left, g, n.left, n, n.right, p, p.right, g);
    } else if (g.left != null && n == g.left.right) {
        balance(p.left, p, n.left, n, n.right, g, g.right, g);
    }
}

private void balance(@Nullable Node<E> a, Node<E> b, @Nullable Node<E> c,
                     Node<E> d,
                     @Nullable Node<E> e, Node<E> f, @Nullable Node<E> g,
                     Node<E> top) {

    if (top.isLeft()) {
        top.parent.left = d;
    } else if (top.isRight()) {
        top.parent.right = d;
    } else {
        root = d;
    }

    b.right = c;
    f.left = e;
    d.left = b;
    d.right = f;

    if (c != null) c.parent = b;
    if (e != null) e.parent = f;

    d.parent = top.parent;
    b.parent = d;
    f.parent = d;

    ((AVLNode<E>) b).updateHeight();
    ((AVLNode<E>) f).updateHeight();
    ((AVLNode<E>) d).updateHeight();
}

3.3 删除节点

删除节点只会导致一个父节点或祖先节点失衡。
因为如果失衡，则被删除的节点必定存在于较矮的子树中，因此失衡节点的高度并没有发生变化。

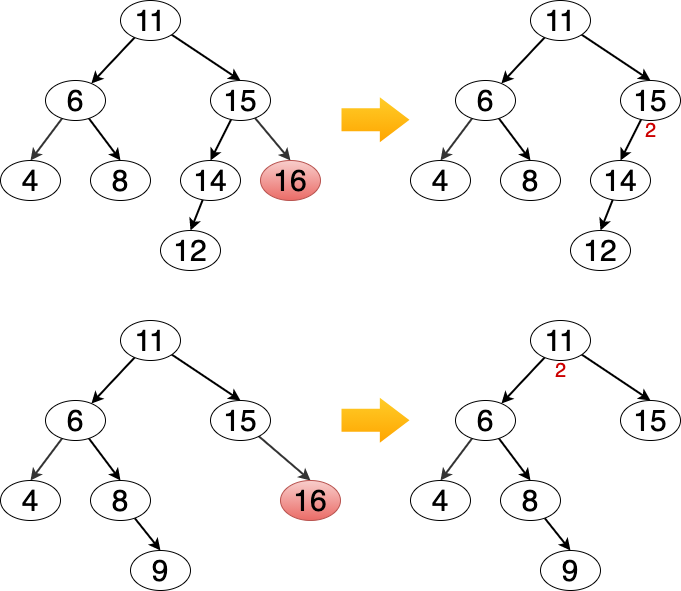
Figure 15: 一个父节点或祖先节点失衡

失衡父节点恢复平衡后，可能 又会导致上游祖先节点失衡 ，最坏情况是所有祖先节点都失衡。(\(O(logn)\))

protected void nodeRemoved(Node<E> node) {
    super.nodeRemoved(node);
    Node<E> g = node.parent;
    while (g != null) {
        if (((AVLNode<E>) g).isBalanced()) {
            ((AVLNode<E>) g).updateHeight();
        } else {
            balance(g);
            // don't break go on loop
        }
        g = g.parent;
    }
}

4 B 树

B 树是一种 平衡多路搜索树 ，多用于 文件系统 和 数据库 。

B 树的定义与约束，主要是对非叶子节点的子节点数量的限制。

4.1 特点

一个节点可以存储多个元素
一个节点可以有多个子节点
每个节点的所有子树高度一致
整体高度相对较低

4.2 m 阶 B 树

m 阶 B 树，指的是任意节点最多拥有 m 个子节点的 B 树。

4.2.1 性质

假设一个节点存储的元素数量为 x ，则：

根节点存储的元素数量 \(1 \le x \le m-1\)
非根节点存储的元素数量 \(\lceil m/2 \rceil - 1 \le x \le m-1\)

假设一个节点的子节点数量为 \(y = x + 1\) ，则：

根节点存储的子节点数量 \(2 \le y \le m\)
非根节点存储的子节点数量 \(\lceil m/2 \rceil \le y \le m\)

4.3 添加元素

新添加的元素必定是添加到叶子节点。

4.3.1 上溢

当叶子节点的元素超过最大数量限制时发生上溢，上溢是唯一能让B树高度增加的方法。

假设上溢节点中间位置为 k ，将 k 位置的元素向上与父节点合并。并将 \([0, k-1]\) 和 \([k+1 , m-1]\) 位置的元素分裂成两个子节点。

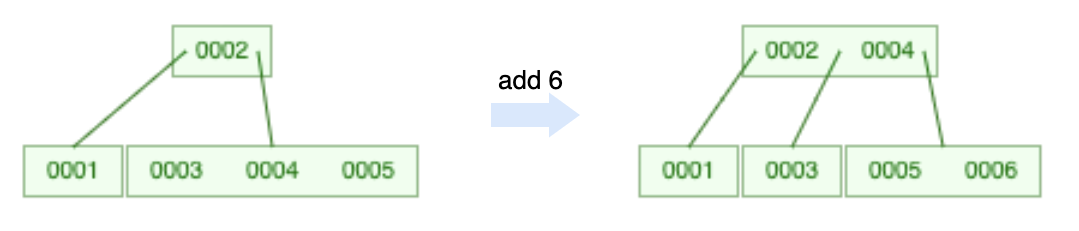
Figure 16: 上溢

4.4 删除元素

4.4.1 元素在叶子节点中

直接删除即可

4.4.2 元素在非叶子节点中

先找到前驱或者后继，用该值覆盖待删节点中的值
删除前驱或后继

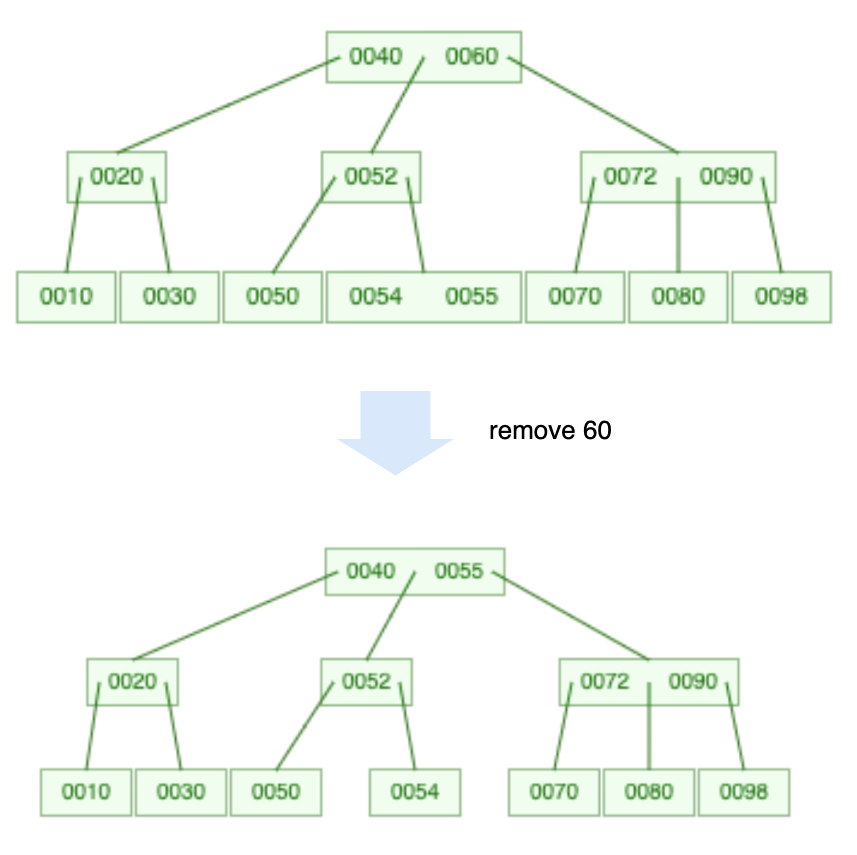
Figure 17: 删除非叶子节点中的元素

B 树非叶子节点元素的前驱或后继必定在叶子节点中。

4.4.3 下溢

当节点的元素数量等于 \(\lceil m/2 \rceil -2\) 时，发生下溢，下溢是唯一能让B上高度减少的方法。

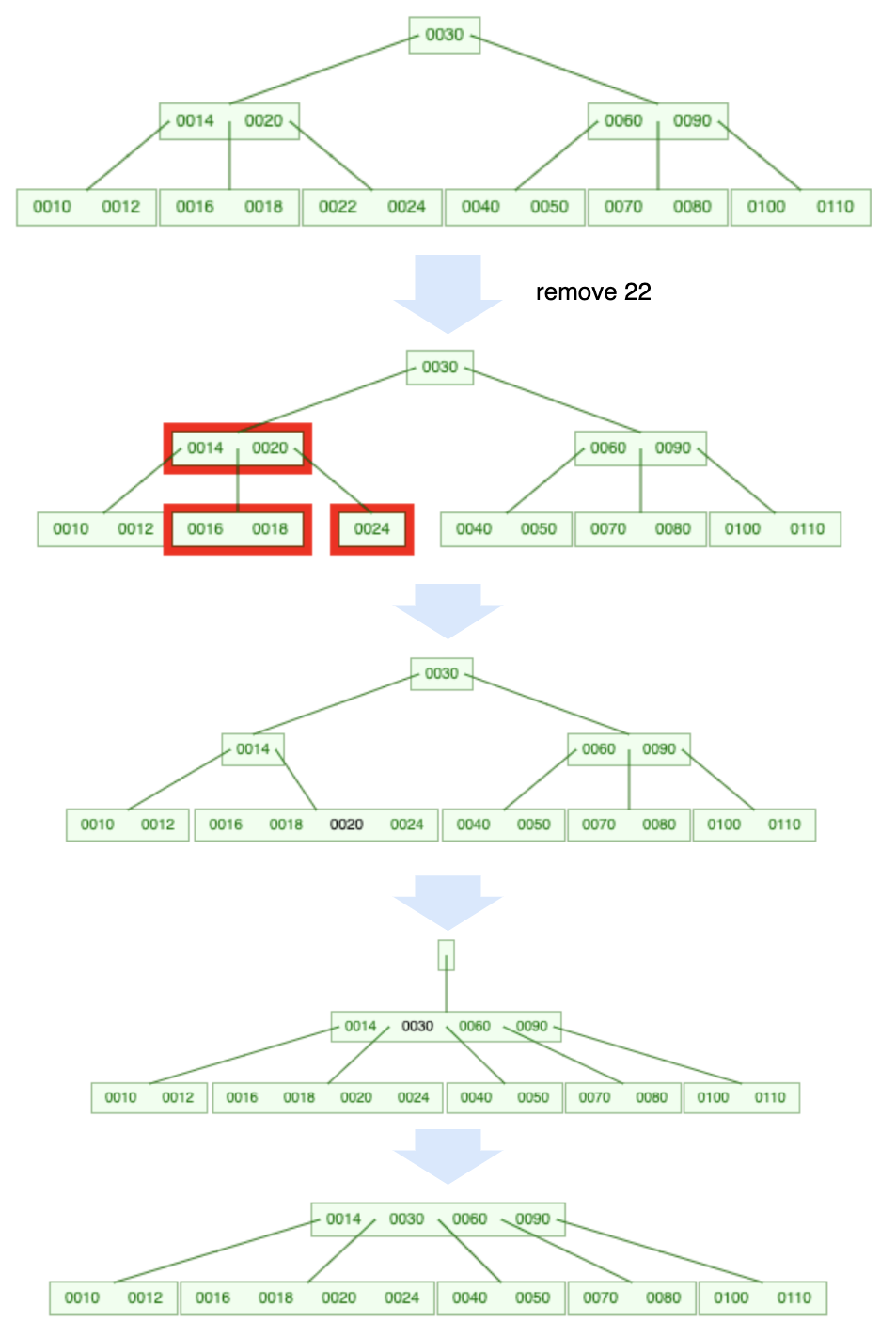
Figure 18: 5 阶 B 树删除元素(5 阶 B 树非根节点元素数量至少为 2)

4.4.3.1 兄弟节点有足够元素

如果下溢节点的临近兄弟节点有至少 \(\lceil m/2 \rceil\) 个元素，可以从中获取一个元素：

将父节点中的元素插入下溢节点 0 的位置
用兄弟节点的最大元素代替父节点中元素

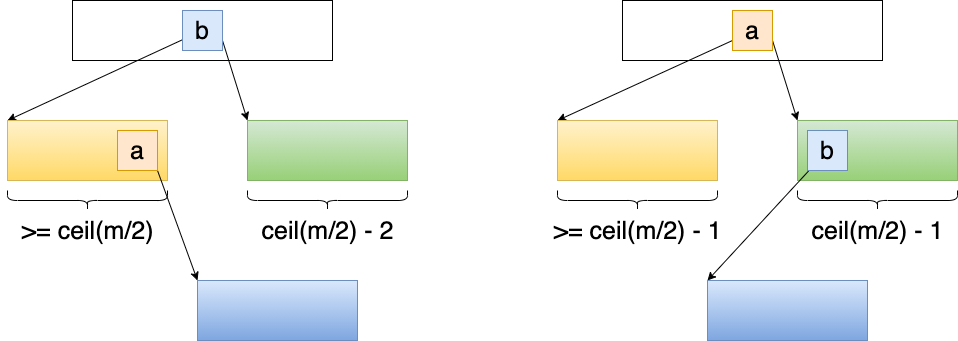
Figure 19: 从兄弟节点中借取元素

4.4.3.2 兄弟节点无足够元素

如果下溢节点的临近兄弟节点元素数量仅有 \(\lceil m/2 \rceil - 1\) ：

将父节点元素取下来，并与左右子节点合并

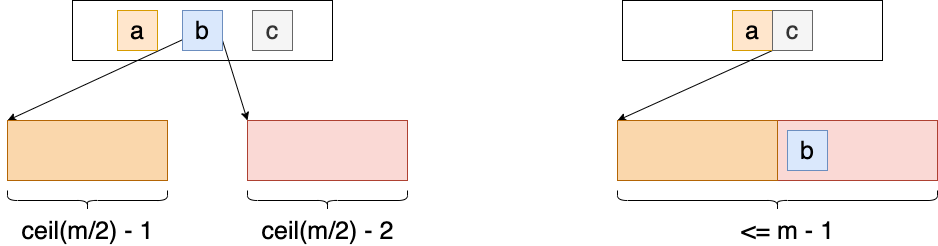
Figure 20: 从兄弟节点中借取元素

5 B+ 树

B+ 树是 B 树的变体，通常用于数据库和操作系统的文件系统中，例如， MySQL 的索引 就是基于 B+ 树实现的。

5.1 特点

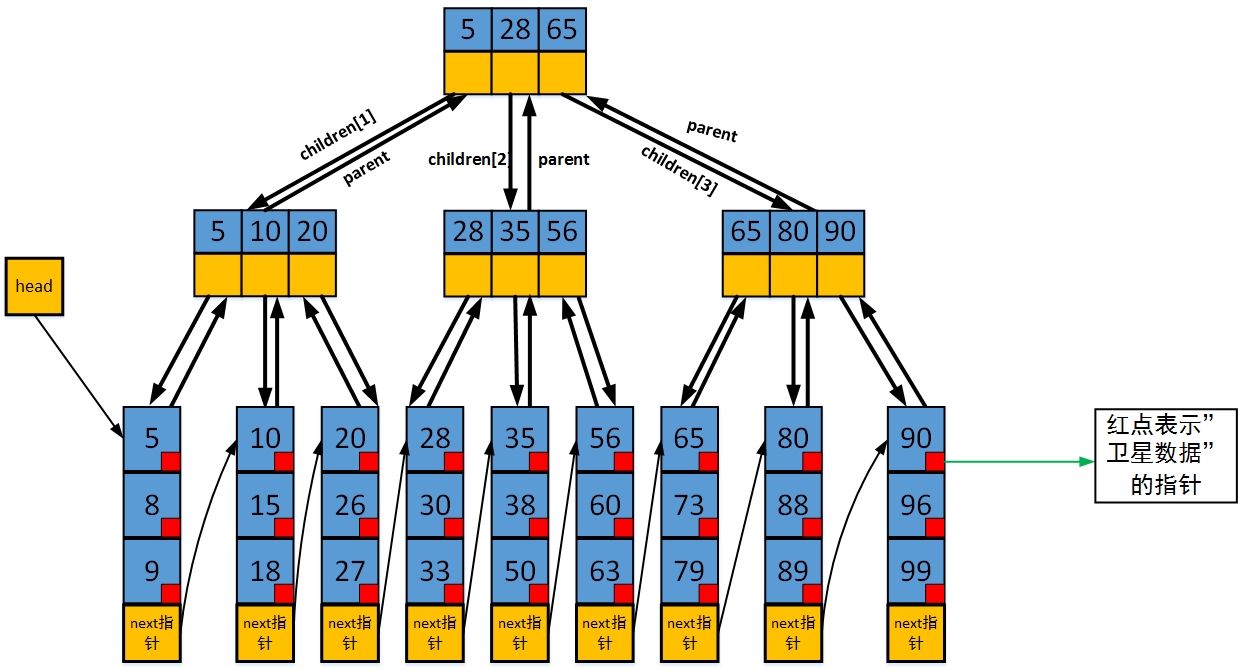
Figure 21: B+ 树示例

分为非叶子节点和叶子节点两种类型的节点，非叶子节点又称为 内部节点
- 内部节点只存储键，不存储数据
- 叶子节点存储键和数据
B 树中一条记录只会出现一次，不会重复出现，而 B+ 树的键则可能 重复出现 ，一定会在叶节点出现，也可能在非叶节点重复出现
B 树中的非叶子节点，记录数比子节点个数少 1 ；而 B+ 树中 记录数与子节点个数相同
所有叶子节点形成一条 有序链表
m 阶 B+ 树非根节点元素数量 x 为: \(\lceil \frac{m}{2} \rceil \le x \le m\)

5.2 数据库为何选择 B+ 树

为了减小 IO 操作数量，一般把一个节点的大小设计成 最小读写单位 的大小。如 InnoDB 的最小读写单位是 16K
因为 B+ 树的非叶子节点只存储键，因此在相同节点大小的情况下，相比 B 树，每个节点存储的 key 数量更多 ，树的高度也因此降低
所有叶子节点形成一条有序链表，适合做 区间查询

6 红黑树

6.1 性质

节点要么是红色，要么是黑色
根节点必须是黑色
叶子节点（空节点，外部节点）必须是黑色
红节点的子节点必须是黑色 (反证可以推断：红节点的父节点必定是黑色)
从 任一节点 到叶子节点的所有路径都包含相同数目的黑色节点

满足这五条性质，红黑树就能保证平衡。

6.2 与 B 树的关系

将红色节点向上与黑色父节点合并，就可以得到等价的 4 阶 B 树。
B 树中每个节点的根节点必为黑色。

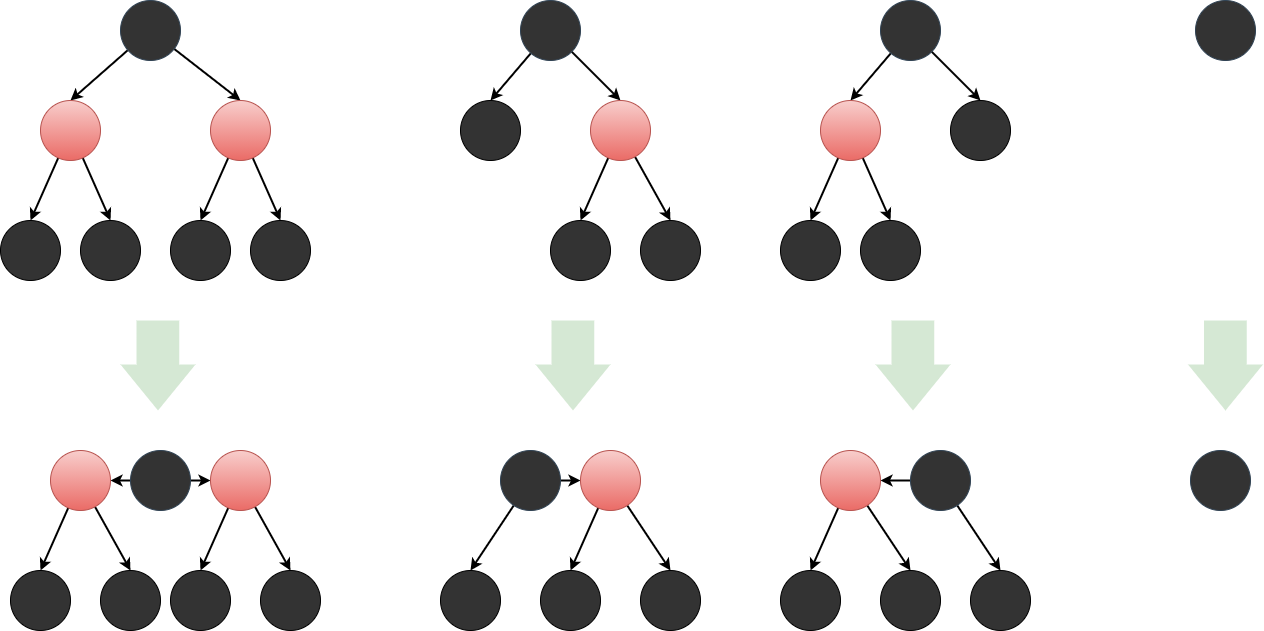
Figure 22: 红黑树转换成 B 树

上图的四种情况，是红黑树转换为 B 树后， B 树节点仅可能存在的 4 种形态。

6.3 添加节点

添加的节点必然是作为叶子节点添加。

添加前倒数第一，第二层的形态只有下面四种：

Figure 23: 添加前叶子的四种形态

因此插入的位置只有 12 中可能：

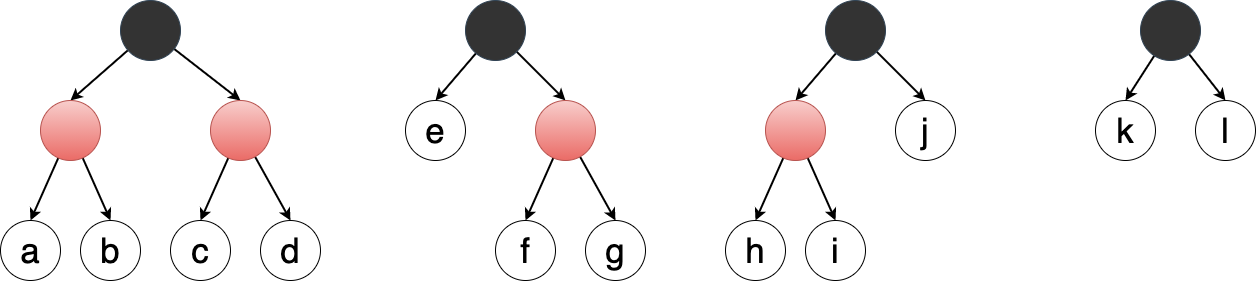
Figure 24: 可添加节点的 12 个位置

6.3.1 父节点为黑色的情况

当父节点为黑色（对应 e/j/k/l 四个位置），直接插入红色节点即可。（不会破坏任何一条红黑树性质）

6.3.2 父节点为红色

6.3.2.1 叔父节点为黑色

对应 f/g/h/i 四个位置，插入红色节点，并通过左右旋转，即可恢复平衡。

// f, g, h, i
if (color(node.uncle()) == Color.BLACK) {
    Node<E> g = node.parent.parent;
    Node<E> p = node.parent;
    Node<E> n = node;
    if (g.left != null && n == g.left.left) {
        red(g);
        black(p);
        rightRotate(g);
    } else if (g.right != null && n == g.right.right) {
        red(g);
        black(p);
        leftRotate(g);
    } else if (g.right != null && n == g.right.left) {
        red(g);
        black(n);
        rightRotate(p);
        leftRotate(g);
    } else if (g.left != null && n == g.left.right) {
        red(g);
        black(n);
        leftRotate(p);
        rightRotate(g);
    }
    return;
}

6.3.2.2 叔父节点为红色

对应 a/b/c/d 四个位置，插入红色节点，并将父节点染成黑色，同时将祖先节点 当做新节点 插入红黑树。

之所以将祖先节点当做新节点插入，是因为现在祖先节点的左右子树都已满足红黑树定义，只要将祖先节点调整到正确的位置即可，而祖先节点的插入位置，必定也是 12 个位置中的一个，因此这里是递归处理的思想。

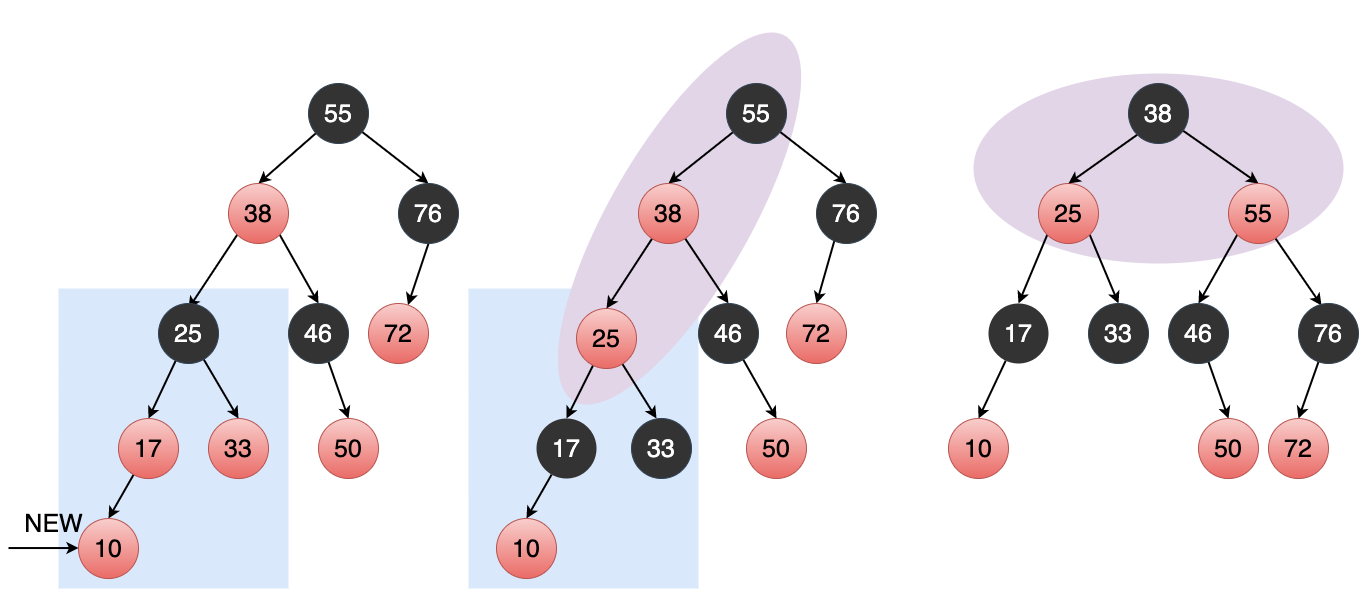
Figure 25: 祖先节点的处理

从上图中可以看出，只要把紫色部分调整好，就完成了整棵树的平衡， 因为除了紫色区域，其余子树都是红黑平衡的 。
而紫色区域的平衡等效于将 25 作为新节点插入。

// a, b, c, d
black(node.parent);
black(node.uncle());
nodeAdded(red(node.parent.parent));

6.4 删除节点

真正被删除的节点必然是度小于 2 的节点，因此红黑树中被删除节点只能存在于倒数第一，第二行：(不包含黑色节点 a)

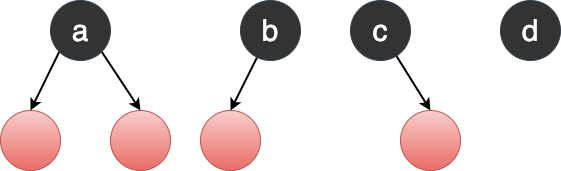
Figure 26: 最后两行形态

6.4.1 被删除节点为红色节点

直接删除即可，删除后仍然满足红黑树性质。

6.4.2 被删除节点为黑色节点

6.4.2.1 非叶子节点

即节点 b/c 的情况，此时将子节点标记为黑色即可。

6.4.2.2 叶子节点

即 d 的情况，也是最复杂的情况， 要结合 4 阶 B 树分析 。

6.4.2.2.1 根节点

不作处理。

6.4.2.2.2 兄弟节点为黑色非叶子节点(能借)

本质上是 B 树下溢的情况。如果兄弟节点为红色的话，则其实在对等的 B 树中对应被删节点的父节点，不能从父节点借。

可以通过旋转并染色来恢复平衡。 旋转之后的中心节点的颜色和被删元素根节点同色，左右节点设为黑色（因为左右节点可以看作独立的 B 树节点）。

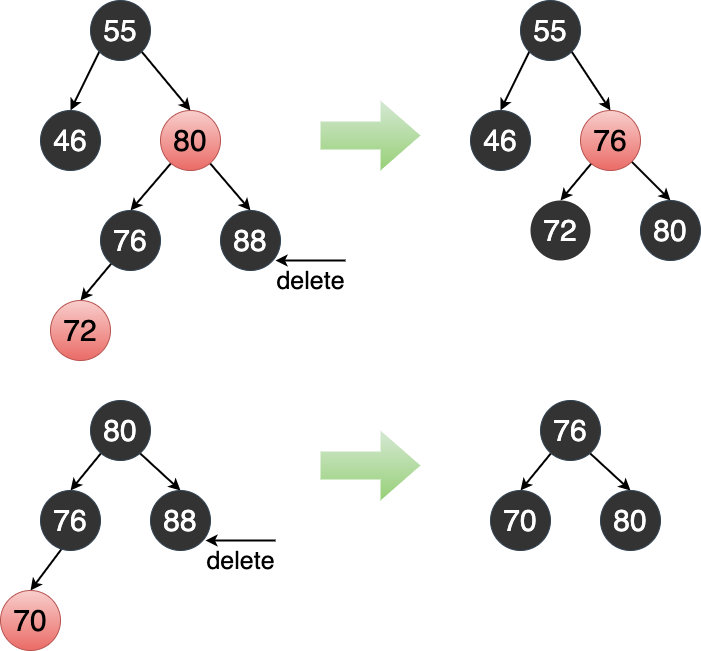
Figure 27: 兄弟节点为黑色非叶子节点的情况(父节点分别为红色和黑色)

6.4.2.2.3 兄弟节点为黑色叶子节点(不能借)

从 B 树的角度看，需要将父节点与兄弟节点合并。

6.4.2.2.3.1 父节点为红色

此时 将兄弟节点设为红色，父节点设为黑色 即可修复红黑树性质。

6.4.2.2.3.2 父节点为黑色

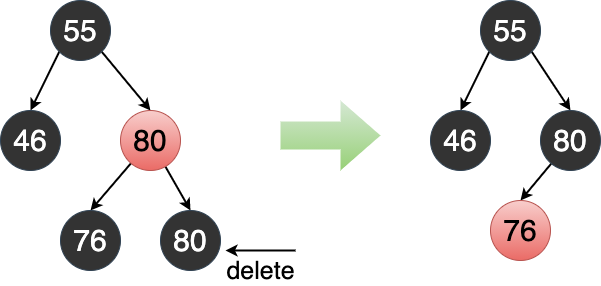
因为已知前提是被删节点的兄弟节点为黑色，因此可推断父节点不可能有红色子节点，从 B 树的角度看是发生了父节点下溢。

从二叉红黑树的角度看，是底部的树发生了失衡。这里可以利用递归的思想， 将父节点当做被删除节点处理 ，从而引发上层树的调整，最终达到平衡整棵树的目的。

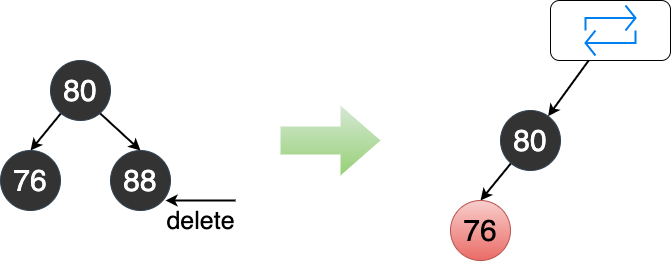
6.4.2.2.4 兄弟节点为红色

将兄弟节点设为黑色，父节点设为红色， 通过旋转使得原先兄弟节点的子节点变为待删节点的兄弟节点 。
旋转之后转换成为兄弟节点为黑色节点的情况。

7 二叉堆

7.1 性质

如果任意节点的值总是大于等于子节点，这样的堆称为大顶堆
如果任意节点的值总是小于等于子节点，这样的堆称为小顶堆
二叉堆是一颗完全二叉树
二叉堆的底层数据结构，一般 使用数组实现

7.1.1 索引(i)规律(n为元素数量)

数组中索引为 0 的元素是根节点
当索引 \(i > 0\) 时，该节点的父节点索引为 \(\frac{i-1}{2}\)
如果 \(2i+1 \le n-1\) 表明该节点有左子节点，且左子节点索引为 \(2i + 1\)
如果 \(2i+2 \le n-1\) 表明该节点有右子节点，且右子节点索引为 \(2i + 2\)

7.2 接口

int size();
boolean isEmpty();
void clear();
void add(E element);
E get(); // 获得堆顶元素
E remove(); // 删除堆顶元素
E replace(E element); // 替换堆顶元素(会触发堆的更新)

7.3 添加元素 \(O(logn)\)

添加元素至数组末尾
如果节点元素大于父节点，则与父节点交换位置
直至节点元素小于等于父节点，或到达根节点位置

Figure 31: 上滤

public void add(E element) {
    elements.add(element);
    siftUp(size() - 1);
}

private void siftUp(int index) {
    if (index == 0) return;

    while (true) {
        int parentIndex = (index - 1) / 2;
        if (parentIndex < 0) return;

        E current = elements.get(index);
        E parent = elements.get(parentIndex);

        if (current.compareTo(parent) < 1) return;
        elements.set(parentIndex, current);
        elements.set(index, parent);
        index = parentIndex;
    }
}

可以优化 siftUp ：即不急着交换，只是先把较小的父节点换下来，当确定最终位置时，才将添加节点的值复制过去。

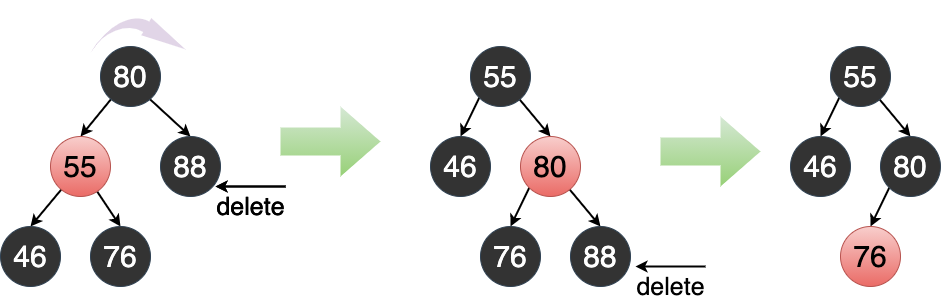
7.4 删除元素 \(O(longn)\)

用最后一个元素的值覆盖根节点的值，然后删除最后一个元素，并对根元素进行下滤 :

如果小于子节点，则与 最大的 子节点交换位置
直至当前节点大于等于子节点或已经成为叶子节点

Figure 32: 下滤

public E remove() {
    if (isEmpty()) return null;
    E root = elements.get(0);
    elements.set(0, elements.get(size() - 1));
    elements.remove(size() - 1);
    siftDown(0);
    return root;
}

private void siftDown(int index) {
    if (size() <= 1) return;
    E current = elements.get(index);
    while (true) {
        boolean hasLeft = (2 * index + 1 < size());
        if (!hasLeft) return; // leaf
        int leftIndex = 2 * index + 1;

        boolean hasRight = (2 * index + 2 < size());
        // int rightIndex = 2 * index + 2;
        int rightIndex = leftIndex + 1;
        int childIndex = leftIndex;
        if (hasRight && elements.get(rightIndex).compareTo(elements.get(leftIndex)) > 0) {
            childIndex = rightIndex;
        }

        if (elements.get(childIndex).compareTo(current) > 0) {
            elements.set(index, elements.get(childIndex));
            elements.set(childIndex, current);
        }
        index = childIndex;
    }
}

7.5 heapify

7.5.1 自上而下上滤 \(O(nlogn)\)

本质是添加操作。

private void heapify() {
    if (isEmpty()) return;
    for (int i = 1; i < size(); i++) {
        siftUp(i);
    }
}

7.5.2 自下而上下滤 \(O(n)\)

原理和删除操作等同。

private void heapify() {
    if (isEmpty()) return;
    int lastNonLeafIndex = (size() / 2 - 1);
    for (int i = lastNonLeafIndex; i >= 0; i--) {
        siftDown(i);
    }
}

8 Union Find (动态连通性)

8.1 存储结构

如果处理的数据都是整型数据，则可以使用数组实现的树形结构来存储数据。

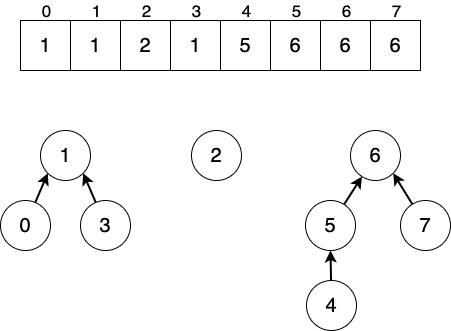
Figure 33: 使用数组存储并查集

8.2 接口

public interface UnionFind<V> {
    // 查找所属集合根节点
    V find(V v);
    // 合并 v1, v2 所属集合
    void union(V v1, V v2);
    // 判断是否连通
    default boolean isConnected(V v1, V v2) {
        return find(v1) == find(v2);
    }
}

8.3 优化查询的实现

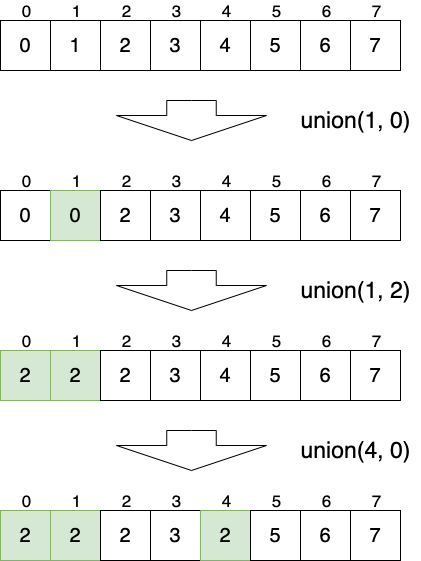
Figure 34: Quick Find 实现

8.3.1 find \(O(1)\)

public Integer find(Integer v) {
    return parents[v];
}

8.3.2 union \(O(n)\)

public void union(Integer v1, Integer v2) {
    int p1 = parents[v1];
    int p2 = parents[v2];
    if (p1 == p2) return; // already connected

    for (int i = 0; i < parents.length; i++) {
        if (parents[i] == p1) {
            parents[i] = p2;
        }
    }
}

8.4 优化连通的实现

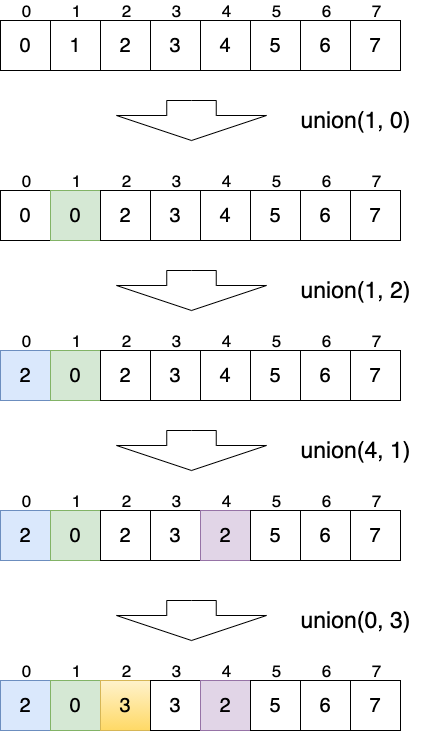
Figure 35: Quick Union

8.4.1 find [O(logn)]

public Integer find(Integer v) {
    while (true) {
        int p = parents[v];
        if (p == v) return p;
        v = p;
    }
}

8.4.2 union \(O(logn)\)

public void union(Integer v1, Integer v2) {
    int p1 = find(v1);
    int p2 = find(v2);
    if (p1 == p2) return; // already connected

    parents[p1] = p2;
}

8.4.3 优化

8.4.3.1 基于 size

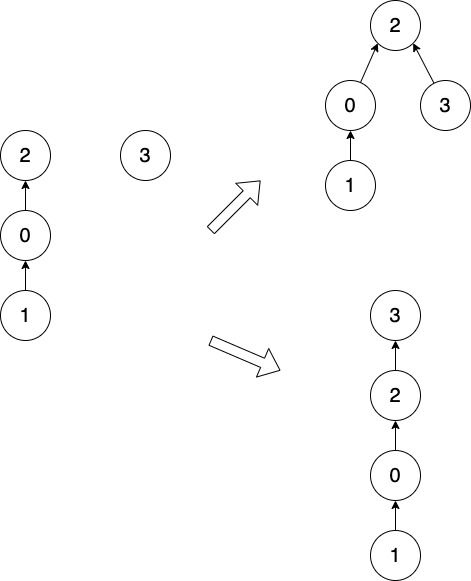
Figure 36: 元素少的嫁接到元素多的

public void union(Integer v1, Integer v2) {
    int p1 = find(v1);
    int p2 = find(v2);
    if (p1 == p2) return; // already connected

    int s1 = sizes[p1];
    int s2 = sizes[p2];
    if (s1 > s2) {
        parents[p2] = p1;
        sizes[p1] += sizes[p2];
    } else {
        parents[p1] = p2;
        sizes[p2] += sizes[p1];
    }
}

8.4.3.2 基于 rank

public void union(Integer v1, Integer v2) {
    int p1 = find(v1);
    int p2 = find(v2);
    if (p1 == p2) return; // already connected

    int r1 = ranks[p1];
    int r2 = ranks[p2];
    if (r1 > r2) {
        parents[p2] = p1;
    } else {
        parents[p1] = p2;
    }
    if (r1 == r2) {
        ranks[p2]++;
    }
}

8.4.3.3 路径压缩

路径压缩的思想是：在 find 时，使路径上的所有节点 都指向根节点 ，以此降低树的高度。

public Integer find(Integer v) {
    List<Integer> indexAlongPath = new ArrayList<>();
    while (parents[v] != v) {
        indexAlongPath.add(v);
        v = parents[v];
    }
    for (Integer index : indexAlongPath) {
        parents[index] = v;
    }
    return v;
}

//    public Integer find(Integer v) {
//        if (parents[v] != v) {
//            parents[v] = find(parents[v]);
//        }
//        return parents[v];
//    }

8.4.3.4 路径分裂 \(O(\alpha(n))\)

而路径分裂的基本思想是：使路径上每个节点都 指向祖父节点 。

该算法的复杂度为 \(O(\alpha(n))\) ，其中 \(\alpha(n) < 5\) 。

public Integer find(Integer v) {
    while (parents[v] != v) {
        int p = parents[v];
        parents[v] = parents[p];
        v = p;
    }
    return v;
}

树 {Back to Index} Expand All Details on Page

Table of Contents